Finding optimal rotation and translation between corresponding 3D points

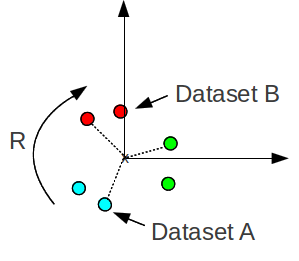
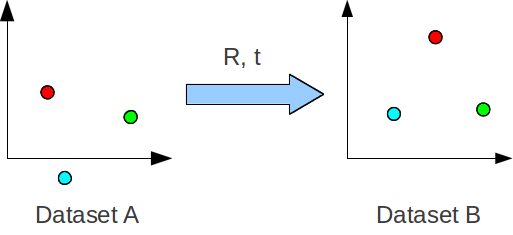
Finding the optimal/best rotation and translation between two sets of corresponding 3D point data, so that they are aligned/registered, is a common problem I come across. An  illustration of the problem is shown below for the simplest case of 3 corresponding points (the minimum required points to solve).

The corresponding points have the same colour, R is the rotation and t is the translation. We want to find the best rotation and translation that will align the points in dataset A to dataset B. Here, ‘optimal’ or ‘best’ is in terms of least square errors. This transformation is sometimes called the Euclidean or Rigid transform, because it preserves the shape and size. This is in contrast to an affine transform, which includes scaling and shearing.

This problem arises especially in tasks like 3D point cloud data registration, where the data is obtained from hardware like a 3D laser scanner or the popular Kinect device.

Solution overview

The solution presented will work with both noise free and noisy data. A minimum of 3 unique points is required for a unique solution.

For noise free data it will solve for

RA + t = B

If the data is noisy it will minimize the least squares error

err = \displaystyle\sum\limits_{i=1}^N \left|\left|RA^i + t -B^i \right|\right|^2

Where A and B are sets of 3D points with known correspondences. R is a 3×3 rotation matrix and t is the translation vector (technically matrix Nx3).

Finding the optimal rigid transformation matrix can be broken down into the following steps:

  1. Find the centroids of both dataset
  2. Bring both dataset to the origin then find the optimal rotation R
  3. Find the translation t

Finding the centroids

This bit is easy, the centroids are just the average of the points and can be calculated as follows:

centroid_A = \frac{1}{N} \displaystyle\sum\limits_{i=1}^N A^i

centroid_B = \frac{1}{N} \displaystyle\sum\limits_{i=1}^N B^i

A^i and B^i are 3×1 vectors eg. \left[\begin{array}{c} x\\ y\\ z \end{array}\right]

Finding the optimal rotation

There are a few ways of finding optimal rotations between points. The easiest way I found is using Singular Value Decomposition (SVD), because it’s a function that is widely available in many programming languages (Matlab, Octave, C using LAPACK, C++ using OpenCV …). SVD is like this powerful magical wand in linear algebra for solving all sorts of numerical problems, but tragically wasn’t taught when I was at uni. I won’t go into details on how it works but rather how to use it. You only need to know that the SVD will decompose/factorise a matrix (call it E), into 3 other matrices, such that:

[U,S,V] = SVD(E)

E = USV^T

If E is a square matrix then U, S and V are the same size as well. We’re only interested in square matrices for this problem so I won’t go into detail about rectangular ones.

To find the optimal rotation we first re-centre both dataset so that both centroids are at the origin, like shown below.


This removes the translation component, leaving on the rotation to deal with. The next step involves accumulating a matrix, called H, and using SVD to find the rotation as follows:

H = (A - centroid_A)(B - centroid_B)^T

[U,S,V] = SVD(H)

R = VU^T

H is the familiar covariance matrix. A - centroid_A is an operation that subtracts each column in A by centroid_A.

At this point you may be thinking, “what the, that easy?!”, and indeed you would be right. One thing to be careful is that you calculate H correctly. It should end up being a 3×3 matrix, not an NxN matrix. Pay close attention to the transpose symbol. It’s doing a multiplication between 2 matrices where the dimensions effectively are, 3xN and Nx3, respectively. The ordering of the multiplication is also important, doing it the other way will find a rotation from B to A instead.

Special reflection case

There’s a special case when finding the rotation matrix that you have to take care of. Sometimes the SVD will return a ‘reflection’ matrix, which is numerically correct but is actually nonsense in real life. This is addressed by checking the determinant of R (from SVD above) and seeing if it’s negative (-1). If it is then the 3rd column of V is multiplied by -1.

if determinant(R) < 0
    [U,S,V] = svd(R)
    multiply 3rd column of V by -1
    R = V * transpose(U)
end if

A big thank you goes to Klass Jan Russcher  for the solution.

Finding the translation t

Now that we have solved for R we can solve for t. Plugging the centroids into the equation mentioned at the start we get

R{\times}A + t = B

R{\times}centroid_A + t = centroid_B

t = centroid_B - R{\times}centroid_A

And we’re done!

Note on usage

The solution presented can be used on any size dataset as long as there are at least 3 points. When there are more than 3 points a least square solution is obtained.

Code

https://github.com/nghiaho12/rigid_transform_3D

Reference

  1. https://en.wikipedia.org/wiki/Kabsch_algorithm

  2. “Least-Squares Fitting of Two 3-D Point Sets”, Arun, K. S. and Huang, T. S. and Blostein, S. D, IEEE Transactions on Pattern Analysis and Machine Intelligence, Volume 9 Issue 5, May 1987

499 thoughts on “Finding optimal rotation and translation between corresponding 3D points”

  1. Great tutorial, you did it very easy to understand 😉 I only have a question. Why do we need to multiply t_new*R_new*C_A instead of t_new*R_new only? Thanks a lot!

    Reply

    1. Thanks for the feedback. To answer your question, the reason is because the rotation, R, calculated earlier assumes the points centroid to be at (0,0,0), hence the extra C_A (which brings points A centroid to the origin). If you read the matrix multiplication from right to left, it is doing the following steps in this order

      1. translate point A’s centroid to the origin
      2. rotate point A
      3. translate point A’s centroid to point B’s centroid

      Reply

  2. this seems almost correct, however i think that t_new should actually just be the affine matrix that shift by the centroid of cloud B, not the difference of the centroids.

    Reply

    1. Thanks for spotting the error out! I had a look at the Octave script I wrote and turns out I implemented it correctly but described it in incorrectly in the post 🙂

      Reply

  3. I have reconstructed a scene using a collection of images. The original scene has 100 points and the reconstructed scene has 100 points. I tried finding the rotation between the two scenes but the function did not work. It returns the exact same points?

    Reply

  4. Sorry I made a mistake in my test code! It’s working perfectly fine! Thanks for this, saved a lot of time for me (“,)

    Reply

  6. Or a more a more understandable paper find under “Least-Squares Fitting of Two 3-D Point Sets” by K.S Arun et. alii (1987 )
    Here tree algorithms for matching two point clouds are explained: SVD, Quaternion as well as an Iterative method.

    Reply

  8. I took A and B as same point set and try to find out the transformation matrix. I am expecting transformation matrix like T = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1].
    %Code
    A = [1 2 3; 4 5 6; 7 8 9];
    B = A;
    T = rigid_transform_3D(A, B);

    I got the transformation matrix like:
    T=[-0.3333 0.6667 0.6667 -2.0000
    0.6667 -0.3333 0.6667 -0.0000
    0.6667 0.6667 -0.3333 2.0000
    0 0 0 1.0000]
    Is it correct or I am getting something wrong?

    Reply

    1. Hi,

      If you do T*[A ones(3,1)]’, you will get B, which is mathematically correct. But your input is degenerate. If you do rank(A) you’ll get 2 (instead of 3), so there are infinite solutions.

      Reply

  9. Hi,

    Thanks for this tutorial. However, it seems that this method is only limited sets of 3D data viewed same plane.

    If I had two cameras at different angles viewing the same three 3D points on a model helicopter, how would I go about finding rotation and translation? Since the triangles wouldn’t be the same shape, would that be an affine transform?

    Thanks

    Reply

    1. Hi,

      The diagrams might be a bit misleading but it’s actually meant to be 3D space. I used this technique to align 3D data from a laser scanner.

      Reply

    2. THANKS！ But if there is another matrix to be sovled? For example, deformation matrix. From A to B, firstly rotate,then translate, last deform, how can I get 3 matrixs respectively through 2 sets of points?

      Reply
  10. Pingback: Python port of rigid_transform_3D.m and first impression using Numpy | Nghia Ho
  11. Pingback: Thought this was cool: Python port of rigid_transform_3D.m and first impression using Numpy « CWYAlpha

  12. Hi,

    Ive been trying to make work your matlab code with a rotated image by 30 degree (only rotation no translation).

    I use a SIFT algorithm to detect common feature points in both images and then I apply your script (with those points as the input points) to try to get the applied rotation (30deg) and I get that a traslation has been applied as well. Im getting the following matrix:

    T =
    0.86651 -0.49916 0 79.111
    0.49916 0.86651 0 -44.818
    0 0 -1 0
    0 0 0 1

    Some of the input points look like this:
    A =

    23.883 166.05 0
    65.38 67.402 0
    102.56 229.35 0
    103.26 206.88 0
    104.89 198.93 0
    129.65 116.17 0
    135.97 171.27 0
    138.26 177.16 0

    B =

    16.976 110.74 0
    102.47 47.257 0
    53.48 204.81 0
    65.257 185.77 0
    70.537 179.81 0
    133.41 120.39 0
    111.33 171.34 0
    110.47 177.29 0

    Could you also please explain how to get the rotated angle from the matrix.

    If you could help me I would really appreciated, ive been fighting with it for hours =)

    thanks!

    Nico

    Reply

    1. First make sure you’re using my latest code. You have a -1 at T(3,3), which looks like the result from the old code. It should be 1. For 2D rotation it’s super simple, the angle is just

      rotation = acos(T(1,1)) or
      rotation = asin(T(2,1)) or
      rotation = atan(T(2,1) / T(1,1))

      I can’t remember if the first 2 takes care of the sign correctly, pretty sure the 3rd one will. Have a look at this page

      http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/geometry/geo-tran.html

      to see how the matrix elements are related to angles.

      Reply

      1. Thanks! Ill try then first the latests version of your code. Btw, where do I get it? Ive just seen only 1 Matlab link above, in the Code section, the .m file.

        Nico

        Reply

        1. It was “quietly” updated around Jan 2013. There’s an additional 3 lines of code to check for the determinant being -1.

          Reply

          1. Ok, so Ive been using the latest version then.

            Still getting than undesired traslation in T…

            Could you please use the upper A and B points and paste how the matrix T you obtain is? Im using Matlab and Photoshop to rotate the Image points so Im pretty sure those points have only been rotated, no translated..

            thanks!

            Nico

          2. I assume photoshop rotates from the image centre, so the translation component reflects this. If there is no translation, then it rotates at (0,0), which is the top-left corner of an image instead.

            Can you paste me your commands if you still think this is not right?

  13. This is your Matlab function I use:

    function T = rigid_transform_3D(A, B)

    if nargin ~= 2
    error(‘Missing parameters’);
    end
    % Skipping error checking of input to reduce code clutter

    centroid_A = mean(A);
    centroid_B = mean(B);

    H = zeros(3,3);

    for i=1:size(A,1)
    H = H + ( A(i,:) – centroid_A )’ * ( B(i,:) – centroid_B );
    % NOTE: the transpose is on A, different to my tutorial due to convention used
    end

    [U,S,V] = svd(H);

    if det(V) < 0
    V(:,3) = V(:,3) * -1
    end

    R = V*U';
    C_A = eye(4,4);
    C_B = eye(4,4);
    R_new = eye(4,4);
    C_A(1:3, 4) = -centroid_A';
    R_new(1:3, 1:3) = R;
    C_B(1:3, 4) = centroid_B;
    T = C_B * R_new * C_A;

    Reply

  14. These points correspond to 2 takes of the same image, so the 2nd ones might be slightly rotated and translated, but very few pixels:

    A =
    50.93 204.53 0
    87.188 1279.8 0
    237.19 600.8 0
    378.9 1601.8 0
    458.8 82.172 0

    B =
    54.005 204.5 0
    90.51 1282.2 0
    240.72 600.69 0
    382.59 1601.9 0
    462.01 81.683 0

    As you see, the matrix T outputs a rotation of 90 degrees. I dont understand it…

    T =

    1 0.00049764 0 2.9901
    -0.00049764 1 0 0.49973
    0 0 -1 0
    0 0 0 1

    Rotation of the 2nd Image in relation to the Original: -89.97148760 degrees

    Reply

  15. These points correspond to the same image, but the second one is rotated by 35deg in PS. So, in theory, the 2nd ones should be rotated, no translated at all:

    A =
    18.923 36.453 0
    56.503 107.54 0
    66.38 68.402 0
    107.61 121.48 0
    130.65 117.17 0

    B =
    38.848 205.02 0
    110.37 241.82 0
    96.319 204.11 0
    160.84 222.91 0
    176.75 207.01 0

    As you see, the matrix T outputs a rotation of -54 degrees and a translation of x= 2.5px and y=186px.

    T =

    0.81716 0.57641 0 2.5138
    -0.57641 0.81716 0 186.27
    0 0 -1 0
    0 0 0 1

    Rotation of the 2nd Image in relation to the Original: -54.80169497 degrees

    Reply

        1. That translation is combination of rotation + 2 other translation. Have a look in the script. There is a variable called ‘t’ (small t). That’s probably what you are looking for.

          Reply

  16. Ive checked, there is not ‘t small’ in your Matlab rigid_transform_3D function , where should it be?

    i really appreciate your help, thanks

    Reply

  18. Firstly, thank you very much for all this work – it’s really helped me!

    Secondly, I’m working with this and having lots of problems with the special reflection case. I’ve found that looking at the determinant on V doesn’t always spot the problem. Is it more appropriate to look at the determinant of the rotation matrix, R? This is det(R) = det(U)*det(V) – remembering that the determinant is equal to that of the transpose. I noticed that det(U) was -1 and det(V) was 1 for a reflection case.

    Thirdly, many thanks in advance for any further help you can provide!

    Kind regards,

    Nick

    Reply

      1. A = [-30.3200 20.7500 0 0;
        0 0 -27.0300 33.4500;
        -7.5000 -7.5000 -7.5000 -7.5000];

        B= [-33.4243 17.2760 -3.3237 1.7730;
        47.8792 42.1348 32.9578 62.1567;
        10.8745 11.6758 -12.4699 40.0464];

        I get det(V) = 1 and det(U) = -1.

        The solution appears as a reflection – the signs of rotations come out all wrong and the
        origin comes out on the wrong side of the centroid.

        The B matrix is measured and has lots of noise on it.

        I changed my code to:

        if det(V)*det(U) < 0
        V(:,3) = -V(:,3) ;
        disp('SVD Special Reflection Case!')
        end

        This seems to have sorted it, but I've got lots more testing to do…

        Cheers,
        Nick

        Reply

        1. That’s very interesting. Let me know how you go and if you find a solution I’ll update the page.

          Reply

          1. I’ve just been reading about how the determinant of a transformation indicates whether the transformation preserves orientation.

            This was helpful: http://mathinsight.org/determinant_linear_transformation

            Basically, if det(T) is negative then the orientation has been flipped. For this to happen, det(R) must be negative; which means that if det(V) or det(U) are negative exclusively, then there will be a flip in orientation giving the reflection case.

            Changing the sign of the 3rd column of V corrects this by changing the direction cosines that make up R to a right handed set rather a left handed set; this is such that R(:,3) = cross(R(:,1),R(:,2)) and not cross(R(:,2),R(:,1)).

            I think this has solved it, thanks to you and Klass Jan Russcher. I wouldn’t have landed on this if not for you guys (and having some sort of (good / bad / delete as appropriate) luck with my datasets).

            Cheers,
            Nick

          3. My solution was:

            if det(R) < 0
            R(:,3) = -R(:,3) ;
            end

            This guarantees that det(T) will be positive, as the relative positions of the centroids have no impact on this.

        2. Hi Nghiaho and Nick i have implemented your method using Unity and ARCore. Thanks a ton it helps me a lot. I had a problem though. When i implemented reflection case by just multiplying the third column of R by -1 sometimes my points flip in wrong direction. It took me a while to figure out it is caused by reflection case. I changed implementation to multiplying third column of V by -1 and recalculating the R, it worked like a charm. I thought you might want to know. Thanks again!

          Reply

          1. Hi Ali,

            I too am working on ARCore and am in need of this method. I saw your comment on StackOverflow and found this page.
            Highly appreciated 😀 I was lost otherwise.

            I have a question in regards to the accuracy, i.e. the rmse. I seem to be getting “okayish” results but I am confident that I am using the same points across both ARCore session, but I never get optimal results. “Everything looks good!” is never printed

            I select the same 5 points – AugmentedImage centre, and the 4 corners of the image, whose 3D co-ords I get through hitTest by clicking on the screen of my mobile.

            Any idea how I could improve this?

          2. The tolerance I used for my test case is 1e-5, which may be unrealistic if you’re using measured points subjected to noise. If you’re dealing with pixels, the tolerance is probably more like 0.5 pixel or so.

          3. Hi nghiaho12,

            thanks for your reply. After a couple of tests, I did find that I get an accuracy of around 0.05 or so. And this is pretty accurate for my use case 🙂

            Any suggestions of how this accuracy could be improved? Just food for thought..

            Increase the number of points that are taken to calculate R and t?

          4. Assuming you have simple noise on your measurements then increasing the points will help produce a more accurate R, and t. You might not see much change in the RMSE though. The only way to decrease that really is if your measurements are more accurate (eg. sub-pixel).

  19. Hi,
    I read your explanation and it was fabulous. But I am having some difficulty in using the code. Could you please specify how to specify the points? My doubt is that say X is the set of 3 points and Y is the same set after applying R and T. How can I get Y back from X, R and T?

    I have been using Y1=R*X+repmat(T,1,3), but after this Y1 and Y are different. Why does this happen, where I am going wrong?? Please help.

    Reply

    1. I’ll definitely modify the code to add better documentation soon. Here’s a working example using random points generated. Actually, somehow I accidentally omitted this code in the Matlab file.

      R = orth(rand(3,3)); % random rotation matrix

      if det(R) < 0 R(:,3) *= -1 end t = rand(3,1); % random translation n = 10; % number of points A = rand(n,3); B = R*A' + repmat(t, 1, n); B = B'; T = rigid_transform_3D(A, B); A2 = T * ([A ones(n,1)]'); A2 = A2'; A2 = A2(:,1:3); % remove the 1's added earlier % Find the error err = A2 - B; err = err .* err; err = sum(err(:)); rmse = sqrt(err/n); disp(sprintf("RMSE: %f", rmse)); disp("If RMSE is near zero, the function is correct!");

      Reply

      1. thanks a tonne!!!…its working perfectly now….tho I have one more doubt….what if i give it 2 sets of 3 random points as input….what u have done is that u have calculated B from A(which is random) using R and T….I am asking what if I make both A and B random….I did try this but I found that the RMSE error was greater,,,about 0.15…is it justified???

        Reply

        1. Yep absolutely. If A and B can’t be aligned “perfectly” it will find the “best” it can, in terms of least squared error. Sort of like the line fitting problem.

          Reply

  20. This is a great, simple write up on a great method for registration.
    I’ve implemented a similar method but wonder if you (or others) might provide insight to my next challenge. I’m honestly not quite sure if it is even possible.
    I am hoping to constrain the problem a bit more to use in a machining/inspection application. In this application, I would like to limit my rotations to only one or two axes and do the same with my translations.
    For limiting translation, this is simple, I think, because rotation and translation are decoupled.
    Limiting rotation: It is simple to limit to one axis of rotation by removing elements of the corvariance (H) matrix to match the desired 2D rotation matrix. Limiting to two axes has presented much more issue.
    Also, I am experimenting with the rotation and translation of the data about some datum other than the centroid. In certain situations, it may not be possible to translate the to the origin before rotation.

    Open and curious to hear thoughts on these!

    Thanks!

    Reply

    1. Ignore my last comment, misread what you wrote. What did you try to restrict the rotation matrix to 2 axes? My first thought would be to optimize for one axes after another. So R = R2*R1. But have no idea if this will work.

      Reply

      1. My first thought was to restrict terms of the H matrix to match what a 3D rotation matrix would look like for 2 axes of rotation but this method often provided reflections. I’ll give your idea a try, not sure if it is going to provide a definite best fit though. Worth a shot.
        Progress on my points:
        1. Limit to one axis of rotation: Just reduce the problem to 2D.
        2. Change center of rotation: Do not align centroids to (0,0,0) as a first step. This method will not produce perfect alignment in most cases but does appear to work.

        The main difficultly I am having is proving a best fit. While outputs can appear to look as such, I’m still not sure if I am finding an optimal solution

        Reply

        1. Could you remap your data such that each point is measured as position along and normal distance from an axis? Finding the transformation between 2 axes should only be a 5 degree of freedom operation – translation (3D) and rotation (2D). Of course, the trick is in the detail… but something like that might work.

          Reply

          1. Hmm not sure myself, I’ll have to take a long think about this one 🙂 Depending on your application, if I was to get stuck on the maths I might be tempted to *cheat* and run some non-linear optimiser eg. Levenberg-Marquardt. If both dataset can be centred to the origin, then you only have to optimise for 2 rotation variables. But where’s the fun in that hey :p

  21. Nick-I like that idea, the 2 axis of rotation case is one which I finding that I think I will rarely see. Still, that approach seems worthwhile and I’ll try and code it up.
    Nghia-I’m trying to be “elegant” for no reason other than that I really like this method and want it to work. I definitely have some “cheating” methods that will work but I think we’re on the same page as to why I don’t what to use them. 🙂

    I tried an iterated aproach to combine two rotations (one per step) but this runs into issue because rotation is order dependent.
    I think all I have really done at this point is to selectively reduce my problem to 2D. This works well if point correspondences are know ahead of time. I am using an iterative process of fitting with a closest point algorithm to determine corresponding point sets at each step. Even with dimensions reduction, I am seeing convergence.

    Reply

  22. Hi All,
    I am trying to use Scanalyze app(http://graphics.stanford.edu/software/scanalyze/) implemented by Kari Pulli in Stanford University for performing global registration. As there is no user manual I am not able to figure out to use this app to perform global registration. If any of you know please let me know steps. Hi Nghia, if you have any idea please let me know.

    Thanks
    ravi

    Reply

  23. Thanks for this explanation. I am a bit confused about something.
    If I have the following two sets of 4 points:
    A= [-503.359 -30.668 1164.350;
    -423.903 -27.747 1226.100;
    -514.524 58.149 1186.300;
    -389.714 65.144 1265.790;];

    B= [-501.205 -30.038 1159.550;
    -422.803 -27.152 1222.950;
    -516.559 58.533 1191.580;
    -390.953 66.119 1270.120;];

    As you can see, the two sets of 4 points are very close to each other
    When I run your method I get results like:

    Rotation =[ 0.9987 -0.0499 0.0071;
    0.0503 0.9955 -0.0798;
    -0.0031 0.0800 0.9968;];

    Trans = [ -8.3652, 120.3392, 1.5959];

    If I compute the error as R*A+t -B, the results are indeed very good.
    However, I really don’t expect to see such a large translation.
    The points are really close to each other, and I would expect almost no translation…
    Any insight would be helpful!

    Thanks!

    Reply

    1. Yes it is a bit unintuitive why “t” is not what you expect. To see why this is the case you have to keep in mind the following operations are executed in this particular order:

      1. rotation around the origin
      2. translation

      The R matrix rotates points around the origin eg. (0,0,0). Have a look at this PDF I quickly whipped together.

      rotation_translation_smiley.pdf

      In that example, the smiley face from data A and B are at the exact same position, but oriented differently. The rotation shifts the point and hence the large translation to shift it back.

      Reply

  24. Maybe I should clarify my question. Given A and B our two datasets and assuming that B has rotated and translated with respect to A, how do I find the transformation matrix between the two such that
    A = H*B

    Thanks!

    Reply

    1. Do you mean a matrix H that combines R and t? Like say if H is a 3×4 matrix such that

      H = [R | t] and B is a 3xN matrix, where the last row is all 1 ?

      Reply

  25. hi,
    your code is very helpful.
    still i have a question.
    after running the code and obtaining the rotation matrix R, how can i extract the rotation angles Roll/Pitch/Heading ?

    thank you for your help.

    Reply

  26. Funny we were looking into a similar story, but for data points in higher (than 3) dimension.

    So let X=A-centroid_A, Y=B-centroid_B
    we have Y=R*X, or alternatively Y’=X’*R’
    To find R’ from a regression or projection point of view you can derive
    R’=inv(XX’)XY’
    Other point of view than SVD, no decomposition.

    Reply

    2. This is how I initially tried to solve this too. I realized that this R found by the least squares approach wouldn’t be orthonormal, so I tried to force it orthonormal using SVD.

      Am = A – centroid_A
      Bm = B – centroid_B
      R_ls = inv(Am) * Bm
      [U,S,V] = svd(R_ls)
      R = U*V’

      but I kept getting strange rotations. Is there a reason we can’t force the least squares solution to be orthonormal?

      Reply

      1. This one is best left to the mathematicians 🙂

        Using the inverse as above will return a general 3×3 matrix that consists of rotation + scaling + shearing + others(?). Recovering just the rotation is probably not straight forward. I’ve once had a similar question about recovering rotation from a general 2D affine transform. From my brief investigation it seems to be possible but under some circumstances only.

        Reply

  28. Hello,
    your code is very helpful and im using it to find the rotation angles on a moving platform.
    i am performing this caculation for a long time series data, lets say i have 3000 measuring epochs and i calculate the rotation angle for every epoch (doing the same calculation 3000 times).
    my question is if its possible to calculate the accuracy of those rotation angles?
    if there is, how?

    at the end i need to have, for every measuring epoch, 3 rotation angle and their accuracies.

    thank you for your help.

    Dany

    Reply

    1. Hi,

      The accuracy is going be as good as your input data, numerical inaccuracies from the code should be negligible. So I guess if you know the error from your input you should be able to propagate that information through. Not sure exactly how on top of my head though.

      Reply

  29. Hi !
    I really like your method and its implementation, simple and quite efficient !
    I have one question : why is the solution it provides optimal, and above all why is it optimal in the least-square sense ? Does it have to do with SVD ?
    best regards,
    Lu

    Reply

    1. Hi,

      Your best bet is to have a look at “A Method for Registration of 3-D Shapes” for a more deeper understanding. I just took their words for it 🙂 In general, anything that solves using SVD is minimising a least square error.

      Reply

  30. Great code. I am just wondering on how to break down the final transformation matrix. For the example with Nico was there only an assumption of rotation in the x-direction? what if there was a rotation is y direction as well? How can I obtain the rotations in all directions from the transformation matrix. I looked at the link to the tutorial but I cannot figure out how to get both the breakdown in translation and rotation given cetroid x,y,z.

    Reply

  31. i am trying to find out how good my rotation and translation are for a rigid body motion problem. how can i do this having started down the SVD path?

    Reply

    1. You can apply the transform and for each point find its nearest point and calculate the distance. Do this for every point and average them, this will give you a good idea of how good the transform is. If your points are noisy you can try the median of the distances instead of the average.

      Reply

      1. Can a covariance matrix be generated for the rotation and translation? What i am doing is implementing point to plane ICP fit.

        Reply

        1. I don’t know about getting a covariance matrix for rotation and translation. I’m familiar with point to plane but never implemented it. Isn’t the error just the shortest distance from the point to the plane?

          Reply

  32. Hi,
    I like the simplicity of this code but I am having a little difficulty in understanding how to obtain the new coordinates. Given a data set A [nx3] and another set B [nx3] the code finds the transformation [4×4] matrix. How is it possible to apply this transformation matrix to data set B so that I can obtain the new coordinates?
    Thanks a bunch,
    Mel

    Reply

    1. The algorithm finds R (3×3 matrix) and t (3×1) vector. It is applied like so:

      B2 = R*A + t

      B2 should be close to B (best least square error). The ‘A’ matrix has to transpose to (3xn) to do the operation above.

      Reply

      1. Oh! I got it thank you. Also the data sets always have to match in size correct? What if you have two sets that you don’t have equal dimensions? Since you are matching based of the centroid then the number of points shouldn’t theoretically matter correct?

        Reply

        1. Yep, each set can have different number of points provided each point in A is paired up with a point in B. Some points with have more than one pairing, but that is okay.

          Reply

  33. How would I pair these? I was considering trying to code the rest of the “smaller” matrix full of zeros but since I am a newbie to matlab its a bit rough.

    Reply

    1. Typically for each point in A you find the closest point (Euclidean distance) in B and pair them up. If A is the larger matrix (eg. 10×3) and B is smaller (eg. 5×3), then you can make a B2 that is 10×3, with duplicate entries.

      Reply

    1. Good Morning,
      Me again and sorry for the constant commenting. I followed your advice but now I am not getting the correct transformation. I have two data sets A and B and have repeated values in the smaller matrix to match that of the larger but now the transformation is wrong. Here is the code i have used of yours with slight modification as well as the data sets used. Any suggestion?

      A= [205.5,890.0,175.0;
      187.5,890.0,175.0;
      169.5,890.0,175.0;
      169.5,870.0,175.0;
      187.5,870.0,175.0;
      205.5,870.0,175.0;
      196.5,880.0,175.0;
      178.5,880.0,175.0;
      196.5,890.0,175.0;
      205.5,880.0,175.0;
      196.5,870.0,175.0;
      187.5,880.0,175.0;
      178.5,890.0,175.0;
      178.5,870.0,175.0;
      169.5,880.0,175.0];

      B=[175.0,890.0,200.0;
      175.0,890.0,187.5;
      175.0,890.0,175.0;
      175.0,870.0,175.0;
      175.0,870.0,187.5;
      175.0,870.0,200.0];

      function [A_Orig,B_Transform] = auto_orientation(A, B)
      %Checking user input
      if nargin ~= 2
      error(‘Error: missing parameters. Please review your inputs.’);
      end

      %Keeping Original Data Sets
      Orig_A=A;
      Orig_B=B;

      %Finding Centroids of Data Sets
      Centroid_A = mean(A);
      Centroid_B = mean(B);

      %Matching Matrix Dimensions
      [ma,na]=size(A);
      [mb,nb]=size(B);

      if ma>mb
      N=ceil(ma/mb);
      New_B=repmat(B,N,1);
      New_B=New_B(1:ma,:);
      New_A=A;
      elseif mb>ma
      N=ceil(mb/ma);
      New_A=repmat(A,N,1);
      New_A=New_A(1:mb,:);
      New_B=B;
      else ma=mb;
      New_A=A;
      New_B=B;
      end

      %Setting up initial matrix
      H = zeros(3,3);
      %Computing matrix for singular value decompositon.
      %Recentering A and B to remove translational component
      for i=1:size(New_A,1)
      H = H + ( New_B(i,:) – Centroid_B )’ * (New_A(i,:) – Centroid_A );
      end
      %Singular value decompostion for optimal rotation
      [U,S,V] = svd(H);
      %Rotation Matrix
      R = V*U’;

      %Checking for special cases of just reflect.
      if det(R) < 0
      fprintf('Reflection detected\n');
      V(:,3)= -1;
      R = V*U';
      end
      %Rotation with respect to reflection.
      R = V*U';

      %Computing translational portion of each Data Set
      t_A = eye(4,4);
      t_B = eye(4,4);
      New_R = eye(4,4);
      t_B(1:3, 4) = -Centroid_B';
      New_R(1:3, 1:3) = R;
      t_A(1:3, 4) = Centroid_A;

      %Transformation Matrix
      T = t_A * New_R * t_B;

      %Apply homogenous coordinates to use Transformation Matrix
      mb2=size(Orig_B);
      B_Ones=ones(mb2,1);
      B_H=[Orig_B B_Ones]';
      %Applying Transformation Matrix
      B_Transform=T*B_H;
      B_Transform=B_Transform';

      %Obtaining the 3D Coordinates for A and B
      B_Transform=[B_Transform(:,1) B_Transform(:,2) B_Transform(:,3)];
      A_Orig=A;

      Reply

      1. Your ‘%Matching Matrix Dimensions’ step is incorrect. For each point you need to find the closest matching point in the other set (smallest distance), not just copy and paste the points.

        Reply

    1. See if the determinant of R is -1 or +1, if it’s -1 there’s a reflection that needs to be corrected.

      Reply

  36. Hello. I have a question..
    When we use SVD to get the rotation matrix, is this matrix rz*ry*rx or other combination.
    I need to know because I want to get yaw,pitch and roll using it.
    Thanks

    Reply

  37. Hello
    Thanks for your article, it helped me a lot!
    I still have one question: Am I right in assuming that you can’t use this method when there’s also a (small) scaling involved (values range from 0,98 to 1,02)? What would you recommend in these cases? Do you maybe know a (scientific) publication which deals with that problem?
    Thanks 🙂

    Reply

    1. Hi,

      I’m not actually sure what happens if the scaling is off a bit. I suspect in practice you might be able to get away with it. I don’t know of any reference on top of my head that deals with this. Some keywords I might start with is ICP + scaling.

      Reply

      1. Thanks for your advice on the keywords, I already found some publications.
        One last question: Have you ever thought about simply calculating the 4×4 transformation matrix (using homogenous coordinates) or the 3×3 transformation matrix and the translation vector with a set of linear equations?
        Do you know if these two solutions are equivalent?

        Reply

        1. I originally wrote the tutorial using 4×4 matrices but later changed to 3×3 + 3×1 vector. They’re both equivalent solutions.

          Reply

  38. Thanks so much, this has helped me quite a bit. Has anyone tried this in C++ with BLAS/LAPACK/ARAMADILLO? I am giving it a shot and will post my results if it works!

    Reply

  39. Thanks for such a nice code and tutorial. I am facing some problem. Explaining properly.
    I have 2 different partly reconstructed point cloud of one 3d model. There is a scaling difference between these 2 reconstruction. This scaling factor is unknown to me. Now I want to merge this 2 model. When I use your code to transform from one point cloud to another and merge both point cloud , I can see the scaling difference. I mean I can see 2 model merged but because of the scaling difference 2 structure separately visible. How can I rectify this problem so after merging there there wont be any scaling error.

    Reply

    1. I haven’t actually tried implementing this but it might be possible to find the average scaling factor via

      1. Do ICP as normal
      2. Re-centre the data again
      3. Calculate the average scaling via: scale = length(A_i) / length(B_i). Where length(A_i), is the length of the point A_i from the origin.
      4. Apply scale to A or B
      5. Undo the centering

      This is a pretty simple approach. I know there are more sophisticted ones out there.

      Reply

      1. Thanks for your reply.
        I know the correspondence between 2 points cloud set, so i think step 1, 2, and 5 is not required. I have tried rest of the steps but did not get expected result. Let me know if I am doing it in right way, or any other thought.

        If you can share any implementation of some sophisticated algo then that would be really helpful.

        Reply

        1. A visitor a while back pointed me to this paper:

          “A System for Video-based Navigation for Endoscopic Endonasal Skull Base Surgergy”

          There’s a bit where it details on scale estimation. I haven’t tried it though.

          Reply

  40. I was wondering if you could give me any ideas on how to register two point sets if the points were NOT corresponding? I have two spare point clouds (around 20 points), but to start I don’t know any other information, just xyz. I’ve been trying iterative closest point, and sometimes it finds ‘the’ solution, other times is gets caught in a local minimum. and sometimes the number of points in each set is not the same. thanks John

    Reply

    1. You’ve pretty much hit the limitation of the vanilla ICP, it requires a “good” initial guess. I don’t know of any good way to solve this other than brute force and some robust criteria (depends on your data).

      Reply

  41. Hi Nghia,

    first of all: big thanks to you! Right now I’m doing an internship in medical image processing, and my first task is to implement the ICP. And your explanation helped me a LOT! If I had, I’d put 3 thumbs up for you.

    But now my question: I’m implementing this algorithm in 2D space, thus for images. Of course my rotationmatrix always looks like this:

    bla bla 0
    bla bla 0
    0 0 1

    The problem I have now is that “special reflection case”. There are iterations where I get a rotation matrix with d<0. But multiplying the 3rd column with -1 obviously doesn't change anything. So do I just multiply the 2nd column with -1? Because I'm not that familiar with the mathematics behind it, I can't really tell if that's the right solution.

    Reply

    1. Hi,

      Glad you found it useful. Ahh the dreaded reflection. I never really got to the bottom of the special reflection case, other than see the “fix” mentioned in some paper.

      Try what you suggested and confirm the results visually, it “feels” right 🙂 If you still have problems let me know.

      Reply

  43. Hi, I think there’s a typo in your “Special reflection case” handling above. To get it to work for me, I had to use
    if determinant(R) < 0
    multiply 3rd column of V by -1
    recompute R
    end if

    which is what your Matlab code actually does, but is different from either version you have in the text of this post!

    Reply

  44. Hi all,

    First of all, thanks for the great tutorial.

    I am trying to write the Kabsch code although following a slightly different procedure and trying to write it in Mathematica software. I am having some problems and I wonder if someone could put a small example with the “A” and “B” data input and then the “err” and “R” outputs (lets consider that no translation is necessary). That way I could find any mistake easily

    Thanks a lot.

    Reply

  45. Hi! I am using this algorithm for some visual odometry stuff, and can’t figure out one thing, may be you can help me?
    Assuming I have these two 3-d points sets, that describe the same static object in the space, which I observed with my stereo camera from different angles. So, coordinates of this points determined relative to the frame of reference of the camera. When I compute R and t for these two point clouds – I get them in cameras frame of reference. Now, how can I compute camera movement with them? As I understand, camera rotation in global frame of reference will be R^-1. But how can I get translation of the camera? It appears to be tc=R^-1 * t, but I can’t understand why! Why I should multiply vector t by R^-1?

    Reply

    1. Where did you get tc=R^-1 * t from? My initial thought is if the camera is at X=(0,0,0) then X2 = RX + t = t, hence translate only t.

      Reply

      1. Don’t forget to apply transformation from camera’s frame of reference to global one, because R and t you get it camera’s frame.
        Well, just draw it for 2d case. Imagine, that we flying around the object and looking at its center, so, that its centroids in camera frame in both cases are equal. So, in camera frame of reference this object just rotates around it’s centroid.
        Rc=R^-1 – this is obvious, where Rc – is camera rotation in global frame. And it looks like tc=(R^-1)x(-t). May be there is mistake, but I can not find it.

        Reply

        1. I’m going to have to solve the same problem, I’m also working on stereo vision. Except my head is a bit tired from watching the World Cup 🙂 I’ll get back to you if I see something different.

          Reply

  46. Hi everyone,

    First of all, thank you for the great tutorial.

    I’m looking to solve the Wahba’s problem, I got your algorithm wrote in C# working pretty well, but now I wish compute weights to some points on 3d space.
    I would be glad for some help about that.

    Thank you and best regards.

    Reply

    1. I’m not too familiar with that problem. But I’m also current working with 3d registration from stereo camera. So I’ll probably need to weight the points too.

      Reply

  47. Nice tutorial…..
    can u also explain the same thing for Affine transform, especially for scaling matrix.
    thanks anyways…

    Reply

    1. This tutorial is not applicable to affine transform. The affine includes more than just rotation and translation.

      Reply

  48. Dear sir,

    Greetings!

    This is rakesh from India. It really simple and interesting to learn about the rotation and translation matrix from your site. Actually i surfed a lot in internet for a couple of weeks to end up in your site.

    I am doing my research on Computer Vision. I would like to emulate a touch screen using Laptop and a Projector. I will use 4 LEDs and a color tracking algorithm to estimate the camera pose and applying it to the 5 th LED which actually acts as a pointer.

    So, all i will have was just a 2D data of the 4 points in camera and a 3D point of the LEDs. Can you guide me in how can i use it to estimate the rotation and translation matrix?

    Regards,
    Rakesh

    Reply

    1. Hi,

      I don’t know what your setup is, but if all the LEDs are on a single plane then have a look at this code I wrote nghiaho.com/?page_id=57

      Reply

  49. Hi,
    I am facing a similar problem but I also do have some scaling factor. In my case I already have a matrix which does the base transformation and I want to find out the rotation, translation and scaling. Could you give me any advise on how to do this?
    Regards,
    Damian

    Reply

    1. Hi,

      Are you saying you have a transformation matrix and want to extra the rotation, translation, scaling from it? Or something else ?

      Reply

  50. Great tutorial! One question about cross covariance matrix H: It should be divided by N or not? (At least this is what the original paper does in (24). “A Method for Registration of 3-D Shapes’, by Besl and McKay, 1992”)

    Thanks a lot!

    Germán

    Reply

    1. You don’t actually need to divide for it to work, but you can if you want to be technically correct since H is meant to be covariance.

      Reply

        1. Not really, never implemented it before. But I guess the obvious thing to do would be to replace the average (for centroid calculation) with a weighted average. And something similar when calculating the rotation.

          Reply

  52. Hello,
    What about rotation around different centers, will it invalidate the algorithm? How can we deal with that?
    Thanks a lot

    Reply

    1. What do you mean? The algorithm will shift all the 3d points so their centers are at (0,0,0) when doing the calculation.

      Reply

          1. Your original problem is that for two sets of 3D points x and y related by x=Ry+T, find R and T. Yes?

            Now what if x and y are related by a rotation along some known point C=(a,b), rather than C=(0,0). What will the output R and T of your algorithm mean then?

          2. If the centre is shifted, the T will change to reflect this. If x and y are 3d points that are related by a Euclidean transform then this algorithm will always output a valid R and T.

  53. Thanks for the tutorial.
    Would you more explain if number of points is more than 3, let’s say 8, where the least square error come to play in your formulations?

    Reply

    1. Can you be more specific? I kind of went over what the least square tries to optimize (the square distance between corresponding points).

      Reply

  55. What about a situation when the two datasets are in two different coordinate system? Would that require me to first transform one coordinate system in such a way that its origin is aligned with the other coordinate system? And only after that start calculating the the rotation and translation for the point cloud.
    Or what would be the approach in this case?

    Reply

  56. Is the rotation matrix and the translation vector out put from the code corresponding to the transform of the centroid A to centroid B and not the Cartesian coordinates of A to B?

    Reply

  57. Hi, Thanks for the tutorial.

    I’m having serious trouble calculating the Covariance Matrix. Every time i use your function i get a 1×1 answer for each bit making a 1*3 matrix….

    Here’s my data and calculations:

    Points:
    A1 = 2,2,0
    A2 = 4,3,0
    A3 = 3,1,0
    B1 = 2,-2,0
    B2 = 1,-3,0
    B3 = 3,-4,0

    Centroids:
    CA = 3,2,0
    CB = 2,-3,0

    (A1 – CA)*(B1 – CB)’ = 0
    (A2 – CA)*(B2 – CB)’ = -1
    (A3 – CA)*(B2 – CB)’ = 1

    My matrix arithmetic wasn’t the best to start with and it’s been a few months since i’ve had to do it.

    I tried to to make 2 3X3 matrices of (Ai – CA) and (Bi – CB)’ and then multiplied them together, but this gave an incorrect rotation matrix (i think) The rotation is a right hand 90 degree rotation of a triangle about the Z axis.

    Any help would be greatly appreciated as i imagine i’ve been having a completely special moment for the past few days trying to work it out!

    Best regards, Ben

    Reply

    1. Swap the transpose so you’re doing (3×1) * (1×3), instead of (1×3) * (3×1).

      eg.

      (A1 – CA)’*(B1 – CB)

      Reply

        1. Not mathematically. I’m more of an engineer, I just implement stuff 🙂 There’s paper that I reference on the page that goes into the maths more.

          A Method for Registration of 3-D Shapes’, by Besl and McKay, 1992.

          Reply

          1. No worries, Engineer myself. I did read the paper but the maths is portrayed in a ridiculously complicated manner, the same as every single paper, ever.

            I used the Octave code you provided and it seems to give the answer thats inverted? again i’m most likely missing something but i’ve tested it a few times with known rotations and it always gives the answer in the opposite (diagonally opposite quadrant)

            E.g if you take a 3D space and 3 points at:
            A1 = 1,1,0
            A2 = 2,2,0
            A3 = 3,3,0

            rotate them 90 degrees right handed to:
            B1 = 1,-1,0
            B2 = 2,-2,0
            B3 = 3,-3,0

            Then input these into the formula given in your last comment, or indeed the octave function, it gives the rotation / translation whatever matrix as:

            R = -0 1 0
            -1 0 0
            0 0 1

            The rotational matrix for a rotation on the Z axis is:
            Cos(th) -Sin(th) 0
            Sin(th) Cos(th) 0
            0 0 1

            This is obviously incorrect, as arcsin(-1) is not equal to arcsin(1)

            And when another point is added on to the A points, say 5,5,0
            its rotational counterpart [5,5,0] * R is given to be -5,5,0 rather than 5,-5,0.

            This is solved by multiplying the answer by -1, therefore multiplying the rotational matrix by -1…. inverse is definitely the wrong term, but you get my point.

            Thanks for the tutorial, its been a big help and i’ll have another look at the paper.
            Ben

          2. The R matrix is correct. You have to do R*[x,y,z]’ not [x,y,z]*R. So for your example in octave

            A=[1 1 0; 2 2 0; 3 3 0]
            R=[0 1 0; -1 0 0; 0 0 1]
            R*A’
            ans =

            1 2 3
            -1 -2 -3
            0 0 0

            The result from “ans” is in column order. It matches what you expect.

  58. Hi,

    thanks for that!

    what can i conclude from a rmse=68? what is the max rmse that still considered as good enough?

    thanks

    Reply

    1. Late reply. It depends on the scale of your points. If all your points are like between [-1,1] then 68 is an error.

      Reply

  59. Hi,

    I am writing some game code, and I used this method to reconstruct the rotation matrix from a model which has been deformed by a physics simulation. (I am doing a sort of verlet-integration style sim). This gives me a very robust rigid body simulation.

    The method is a bit math heavy for games work, but it worked fine.

    Until, that is, I plugged in some different models, and then occasionally the SVD spits out a V matrix with a determinant of zero. This looks very odd, because the input matrix is virtually identical to one which produces a valid outcome. It could be a bug in the SVD implementation, which I did not write myself.

    However, I am thinking there might be a simpler solution. If you consider a rotated cube, it would not be hard to reconstruct a 3×3 matrix by looking at the cube’s edge vectors and generating orthogonal i,j,j vectors. You could derive a rotation matrix very cheaply.

    I am wondering whether this methodology could be applied to arbitrary geometry by extracting i,j and k using weighted sums of edges?

    Reply

    1. Hi, You could use the Quaternion method of Horn instead of this method. Then instead of SVD you just find the eigenvectors of a 4×4 symmetric matrix, which is about 30% cheaper than SVD of 3×3 matrix. Also you don’t have to worry about handling special cases like reflections as in the SVD method.

      Check the Horn original paper:

      http://people.csail.mit.edu/bkph/papers/Absolute_Orientation.pdf

      A C++ implementation can be found here:

      https://searchcode.com/codesearch/view/15567732/

      Reply

  60. Hello all

    I’m looking for transformation parameters to align two sets of points and this function looks perfect.
    For my application I need result in form of (trans.x, trans.y, trans.z, rot.x, rot.y, rot.z)
    How can I calculate rotation about each axis from the rotation matrix?

    Thanks
    M

    Reply

  62. Hi, I sent you an email to discuss how to apply this technique to my problem, which is very similar to what you described.

    Thanks for the post and nice blog!

    Reply

  64. Hi there,

    thanks for the tutorial. Very useful! I’m trying to implement a landmark constellation matching algorithm based on this in Python.

    I downloaded your python source code and I think I may have found an error:

    in line 22, the matrix implementation needs to be implemented with Numpy’s dot() function instead of the ‘*’ operand. Otherwise, you get a Nx3 marix instead of a 3×3 matrix.

    Cheers and thanks for all your work!
    -Silvio

    Reply

  65. Hi nghiaho.. your work is awesome and is helping me alot.I am working on Visual odometry and using (rigid_transform_3d.m).

    But please help me. I will explain my problem in short.
    1.I use your function (rigid_transform_3d.m) to find relative rotations(delta R) and relative translations(delta t) between consecutive images.
    2.Thus,for a sequence of 300 images,I obtain 299 delta R and delta t.
    3.now,while plotting position of vehicle, I use

    pos{i}=delta_R{i-1}*pos{i-1} +delta_t{i-1};

    but results are in camera coordinate system. Can you suggest me the way to convert in world coordinate system?

    Reply

    1. I remember doing a similar exercise. This is how I did it

      globalR initialize to 3×3 identity, and globalT to [0;0;0]

      // repeat for all images
      globalR = R*globalR
      globalT = R*globalT + T

      pos = -globalR.transpose() * globalT <-- plot this

      Reply

  66. Hi,
    Thank you for your very didactic tutorial.
    I re-used the code to adapt it to my application.
    I have to adjust 3D tomography images (The experimental configuration suggests that we are in a case of a 3d rigid transform and between two images, the object is mechanically rotated with a known angle + slight unwanted movements).
    So, I select manually a set of common points between two images. Then I inject the coordinates of this points in A and B to find the rotation matrix and the translation vector.
    From these results, I reconstruct the 3D transformation matrix (4×4) :
    [ R R R T]
    [ R R R T]
    [ R R R T]
    [ 0 0 0 1 ]
    Where R corresponds to the rotation matrix and T to the translation vector.
    I apply this transformation to the 3D image corresponding to the A set. After addition of the images “A” and “B” everything seems to work perfectly and the selected points seems to be well placed. However, the rotation angle found is doubled compared to the angle that the object physically done.

    Strange, isn’t it ?

    Reply

  67. Hi Nghiaho,

    Thanks for this post. Actually I need to find angle of rotation between two 3D point clusters so I am using this post to find Rotation matrix and http://nghiaho.com/?page_id=846 to find angles. However, the angles are a little weird.

    So for debugging purposes I tried to find Rotation matrix between y=x ([0,0,0], [1,1,0]….) and x axis ([0,0,0], [1,0,0]…). I initialized 50 points in each group. However, the Rotation matrix I got has a determinant of 0?? Any idea what could be the problem?

    I have implemented this in Java and OpenCV. I haven’t tested your code since I don’t have Octave or Matlab. Here is the Rotation matrix I got :

    [0.70710677, 0.70710677, 0;
    -9.7000784e-016, -9.7000784e-016, 1;
    -0.70710677, -0.70710677, -1.3717982e-015]

    Reply

    1. Hmm without any code hard to say. I’d check line by line with my Octave code. Octave is free on Windows and Linux and maybe Macs, so it’s quick to test.

      Reply

      1. It seems the svd generated in OpenCV is different than the one generated in Octave.
        My H :
        [10412.5, 0, 0;
        10412.5, 0, 0;
        0, 0, 0]

        OCTAVE :

        U =
        -0.70711 -0.70711 0.00000
        -0.70711 0.70711 0.00000
        -0.00000 0.00000 1.00000

        S =
        1.4725e+004 0 0
        0 0.0000e+000 0
        0 0 0.0000e+000

        V =
        -1 0 0
        -0 1 0
        -0 0 1

        OpenCV:

        S: [14725.499;
        0;
        0]
        U: [0.70710677, -9.7000784e-016, -0.70710677;
        0.70710677, -9.7000784e-016, -0.70710677;
        0, 1, -1.3717982e-015]
        V: [1, 0, 0;
        0, 1, 0;
        0, 0, 1]

        This is strange, anyway to handle this?

        Reply

          1. I have constructed 2 3XN matrices A & B for the points. I am calculating the mean of each row and then creating a 3X1 vector for each of the two matrices. Then I subtract that from each column of A & B respectively. This creates two matrices AA and BB of 3XN each again.

            Then I calculate H as AA*Transpose(BB)

  68. Hi Nghaiaho =)

    This is a great page, it really helps me a lot!

    I want to implement an 2D Registration algorithm (not just set the 3rd dimension = 0).
    Can I simplify all different 3D algorithms (e.g. your SVD or Quaternions, Orthonormal Matrices) to 2D differently or is there only one optimal algorithm for two dimensions?

    I found one here ( http://hss.ulb.uni-bonn.de/2006/0912/0912.pdf ) at the bottom of page 133 of the pdf ( = page 112 of the paper). But to what is this corresponding in 3D? It looks similar to SVD, but I’m not sure.

    Kind regards, Niklas =)

    Reply

    1. I’ve never implemented a 2D version of this algorithm. But I’d imagine the 2D version to be pretty simple, without the use of SVD, since you only need to solve for a single theta angle. If you re-centre both datasets then you only need to find the angle theta to rotate point set A to B. For each point pair you can form a vector such that

      A_vector = (0,0,0) -> (Ax, Ay, Az)
      B_vector = (0,0,0) -> (Bx, By, Bz)

      Figure out the angle between the two vectors. Do this for every pair and average them out.

      Reply

  69. Hi NghiaHo,

    Somehow not able to reply to that thread so continuing here,
    I’m writing in Java

    Matrices (3×50):

    A
    [ 0, 1, 2………..49
    0, 1, 2…………49
    0, 0, 0…………….]

    B
    [ 0, 1, 2………..49
    0, 0, 0…………..0
    0, 0, 0…………….]

    for(int i=0; i< points1.rows(); i++)
    centroid1.push_back(rowMean(points1.row(i)));

    for(int i=0; i< points2.rows(); i++)
    centroid2.push_back(rowMean(points2.row(i)));

    ( rowMean is a custom function, it is calculating the correct mean per row, if you want I will post the code )

    Mat points1Centered = new Mat(points1.size(), points1.type());
    for(int i=0; i < points1.cols(); i++)
    Core.subtract(points1.col(i), centroid1, points1Centered.col(i));

    Mat points2Centered = new Mat(points2.size(), points2.type());
    for(int i=0; i< points2.cols(); i++)
    Core.subtract(points2.col(i), centroid2, points2Centered.col(i));

    Core.gemm(points1Centered, points2Centered.t(), 1, dummy, 0, H);

    Core.SVDecomp(H, S, U, V);

    Core.gemm(V, U.t(), 1, dummy, 0, R);

    Reply

      1. What do you mean by legit?
        Well A is just y=x and B is just the x axis, so the angle of rotation between them should be 45 degrees around the z axis.

        Reply

          1. Yes

            I have now tested this fully in Octave. Octave is producing the expected result of angles : 0, 0, 45.

            With these points the H in Octave is the same as the H that Java code is generating. The difference comes after svd. The results of svd are different in java OpenCV and Octave. And I don’t know why 🙁

          2. I think the answer is actually correct even though it looks wrong. The singular values returned are [1.4725e+04, 0, 0]. The last two singular values are numerically identical (0), so the 2nd/3rd column vectors of U can be ordered in either way. In your case, they’re just swapped. If you proceed to continue with the calculation what result do you get?

          1. Oh, Well yes that makes sense. However when I calculate R in OpenCV this is the result :

            [0.70710677, 0.70710677, 0;
            -9.7000784e-016, -9.7000784e-016, 1;
            -0.70710677, -0.70710677, -1.3717982e-015]

            Determinant is 0

            In Octave R comes out as

            0.70711 0.70711 0.00000
            -0.70711 0.70711 0.00000
            0.00000 0.00000 1.00000

            determinant is 1.

          2. Can I just swap second and third rows whenever the determinant is 0? Will that work?

          3. Actually I just realised you have a degenerate set of points. You have a line in 3d space, which has one degree of freedom to rotate around the axis. The algorithm works if your points form a triangle instead.

  70. not sure if someone else has commented on this, but i think there is an error in your mapping in your code. in thinking about it, you need to subtract the source centroid off the points before applying the rotation, then when you add the offset, you still need to add back the source centroid.

    You have :

    Y = Rotation * X + Offset

    What makes better sense is

    Y = Roation * (X-SourceCentroid) + Offset + SourceCentroid;

    Otherwise, if the points are distant from the origin, then you are rotation about the origin an they will have a significant offset added to them.

    The Rotation matrix was computed for rotation of points with their source centroid subtracted – so it only makes sense to apply them to the points of the same condition.

    Reply

    1. and in case it helps others – here’s a C# implementation of the Kabsch Algorithm (which you describe). Look up the wikipedia page for an explanation of variables. P,Q, and the centroids are computed outside this function

      this uses the emgu openvc svd code for 2D rotation. Easily extensible to 3 dimentions by defining the matrixes as 3×3 and making m[1,1] to m[2,2]

      {
      var p = P;
      var q = Q;

      //1. subtract centroids
      for (int i = 0; i < p.Rows; i++) {
      p[i, 0] -= SourceCentroid[0, 0];
      p[i, 1] -= SourceCentroid[1, 0];
      q[i, 0] -= DestCentroid[0, 0];
      q[i, 1] -= DestCentroid[1, 0];
      }

      //2. compute covariance matrix
      var a = p.Transpose()*q;

      //3. compute rotation matrix
      /* perform svd where A = V S WT */
      Matrix V = new Matrix(2, 2);
      Matrix S = new Matrix(2, 2);
      Matrix W = new Matrix(2, 2);
      CvInvoke.cvSVD(a.Ptr, S.Ptr, V.Ptr, W.Ptr, SVD_TYPE.CV_SVD_DEFAULT);

      // Deal with reflection matrix
      Matrix m = new Matrix(2, 2);
      m.SetIdentity(new MCvScalar(1));
      m[1,1] = ((W*V.Transpose()).Det<0) ? -1 : 1;

      // Comput the rotation matrix
      Rotation = W*m*V.Transpose();
      Offset = DestCentroid – (Rotation * SourceCentroid);
      }

      Reply

  71. woops, offset is computed incorrectly. should be

    Offset = DestCentroid – SourceCentroid;

    and the mapping is

    Y = Rotation * (X-SourceCentroid) + Offset + SourceCentroid;

    Reply

  72. Dear Nghia,
    Thank for your post!
    Currently I have similar problem:
    There are 2 similar objects (their sizes might be different, i.e big/small objects). From these objects, we find 2 sets of corresponding points (s1, s2) with the same number of points.
    The mission is to find the transform matrix from s1 –> s2.
    But the transform matrix contains only translation and rotation, not scaling!
    Actually, the complete transform should include scaling. But in my problem, original objects (obj1, obj2) have different sizes.
    And I don’t need scaling because I want to know how different they are.
    I see in your solution, after transformed, two sets are nearly identical to each other.
    For my problem, after transformed, two sets are uniform, but not exactly the same.

    Could you please help?
    Thank you in advance!
    Tom

    Reply

    1. Hmm, I never worked with points that involved scaling so I’m not of any help. Maybe someone else on this site has.

      Reply

      2. When I test your python code with my data, t is not the column vector (2×1), it has 2 columns (2×2).
        My data is 2D matrix (12×2)
        Do you have any suggestion?
        Thanks

        Reply

  73. many thanks for your simple explanation and codes,
    I will use it in my dissertation, I hope it gives me the best.
    if I use I want to have your name in the code, then I should write Nghia Ho?
    be successful in whole your life.
    regards

    Reply

  74. Hello,I have a problem about ‘t’,translation vector I hope you help me:
    in my project I can obtain pose of e.g points with respect to one camera(x,y,z),by help of stereo vision.
    then I want to know R&t of one pose of a plate with respect to another pose of it. I use your code and I can survey correctness of ‘R’ by obtaining the angles(around x,y,z) with this formula:
    http://persian-expert.com/up2/uploads/1438845512991.png

    for verification my target is a board with a triangle on it,the points of corner of triangle are our markers.
    but I have problem with ‘t’, don’t know how to verify it?because I don’t know which distance it represents, for more explanation please go to:
    http://www.persian-expert.com/up2/uploads/1438846564971.jpg

    camera in the image, is left camera(the reference). we have just rotation around y axis. I did some measurements in practice(r1,r2,…in image obtained, by stereo) and also I know the angle and distance of posesA&B to each other priori(for distance e.g I change the place of one corner of rectangle in arbitrary but known distance on the board, and for rotation I rotate the board itself in known angle), and the aim is just verification of my project.
    questions:
    1.when I change point sets on the board(e.g mean points of triangle’s lines) , ‘t’ changes (consider the poses(poseA&poseB) don’t change just markers or three points on the board change), why t changes?
    2.’t’ is distance between origin of coordinates in two coordinate frames, isn’t it?as I don’t know origin for poseA and poseB, how to verify t?
    at last what does ‘t’ represent?
    sorry because of long explanation.
    thank you in anticipation.

    Reply

    1. What you wrote is kind of confusing to read. But if you want to know the translation between the origin of the two sets, use -R’t (negative R transpose multiply t).

      Reply

      1. I tried to explain with details.
        ok let me please:
        what does T vector show?
        I read that it is distance between origin of two set points.
        thanks

        Reply

        1. The transform applies a rotation first, then translation (t) after to align the set of points. So you can’t read ‘t’ directly to measure distance. You need to use -R’*t.

          Reply

    1. Not really, visual odometry is more 2D<->3D pose estimation. This method is only really suitable for 3D<->3D.

      Reply

  77. please help me in this case

    the target point set is generated from rotation and translation of the origin point set.

    but the algorithm seems not giving the correct answer.

    origin：
    Point3D(-12.267, -76.253, 21.673),
    Point3D(-12.711, -76.638, 20.299),
    Point3D(-13.713, -75.658, 19.711),
    Point3D(-14.463, -75.997, 18.788),

    target：
    Point3D(-12.137, -76.147, 21.373),
    Point3D(-12.362, -76.959, 20.14),
    Point3D(-12.498, -76.172, 18.847),
    Point3D(-12.624, -77.053, 17.755),

    Reply

  78. please moderate this:
    hello, please register my question very soon.
    I have a problem in the reason of using SVD method,
    I understand the method up to covariance (H),but why we use SVD? snd then why we use R=V*U’?
    i just want to write very short reason in my dissertation,so I ask this. the code was useful at all.
    thank you

    Reply

  79. Hi,

    amazing post, thanks you very much for sharing. I have successfully been using this code for some time now, but I also fell in the ‘reflection trap’. If no reflection is encountered , the RMSE is for my data around 1e-09 and the reconstruction is optimal. However, when I find a reflection, the reconstruction is somehow not correct.

    Example where everything goes right
    pA = [[ 0.41 0. -0.28991378]
    [-0.41 0. -0.28991378]
    [ 0. -0.41 0.28991378]
    [ 0. 0.41 0.28991378]]

    pB = [[ 0.86974133 0.28991378 0.86974133]
    [ 0.28991378 0.86974133 0.86974133]
    [ 0.86974133 0.86974133 0.28991378]
    [ 0.28991378 0.28991378 0.28991378]]

    Rotation
    [[ 0.70710678 -0.70710678 0. ]
    [-0.70710678 -0.70710678 0. ]
    [ 0. 0. -1. ]]

    Translation
    [[ 0.57982756]
    [ 0.57982756]
    [ 0.57982756]]

    Reconstruction
    [[ 0.86974134 0.28991378 0.86974134]
    [ 0.28991378 0.86974134 0.86974134]
    [ 0.86974134 0.86974134 0.28991378]
    [ 0.28991378 0.28991378 0.28991378]]
    RMSE: 4.47992254088e-09

    I there is a reflection, I get
    Points A
    [[ 0.41 0. -0.28991378]
    [-0.41 0. -0.28991378]
    [ 0. -0.41 0.28991378]
    [ 0. 0.41 0.28991378]]

    Points B
    [[ 0.28991378 0.86974133 0.86974133]
    [ 0.86974133 0.28991378 0.86974133]
    [ 0.86974133 0.86974133 0.28991378]
    [ 0.28991378 0.28991378 0.28991378]]

    Rotation
    [[-0.70710678 -0.70710678 0. ]
    [ 0.70710678 -0.70710678 0. ]
    [-0. -0. 1. ]]

    Translation
    [[ 0.57982756]
    [ 0.57982756]
    [ 0.57982756]]

    Reconstruction
    [[ 0.28991378 0.86974134 0.28991378]
    [ 0.86974134 0.28991378 0.28991378]
    [ 0.86974134 0.86974134 0.86974134]
    [ 0.28991378 0.28991378 0.86974134]]
    RMSE: 0.579827557986

    And you see that the Reconstruction does not match Points B.
    Interestingly, the RMSE is equal to the components of the translations.

    I do handle the reflection as suggested
    if linalg.det(R) < 0:
    Vt[2,:] *= -1
    R = Vt.T * U.T

    Any ideas on this? Cheers!
    Guido

    Reply

    1. I haven’t spent too much verifying the reflection correction. Maybe someone will know the answer. What is the effect of applying the reflection correction?

      Reply

  81. I think there is a typo in the documentation of the special reflection case. You write “This is addressed by checking the determinant of V …” while the code checks the determinant of R:
    if determinant(R) < 0

    Reply

  82. One more thing, when given the following input data:
    A = [0, 0, -25; 0, 0, 25; 25, 0, 0];
    B = A;
    the reflection case handling suggested by Nick Lambert actually returns a 180° rotation even though the data sets are equal.

    Reply

  83. Hi, nice article. I am using two 3D point cloud of different sizes. Fixed one is 3×40256 and moving one is 3×40096 (stanford Bunny). Can you please elaborate how to find closest point between these two ?

    Reply

  84. I tried something a bit different and it didn’t work. I would like to hear your thoughts as to why it didn’t.

    In your program, you have..
    H = (A – repmat(centroid_A, N, 1))’ * (B – repmat(centroid_B, N, 1));

    I tried..
    H = (B – repmat(centroid_B, N, 1))’*pinv((A repmat(centroid_A, N, 1))’) ;

    Reply
  85. Pingback: Python:python implementation of 3D rigid body translation and rotation – IT Sprite
  86. Pingback: ICP algorithm | charmie11

  88. Hi,

    I am trying to develop an algorithm for robotic handling of cuboidal baggage. I want to limit my pose estimation problem to a 2d one by considering one rotation angle theta, and two translation parameters .. Since cuboidal objects exhibit 180 degree rotational symmetry, there are finite poses possible (pose classes). My goal is to implement the chamfer matching process by minimizing the euclidean distance between the stored pose template shapes and the current image scene. I would like to seek your advice on the following :

    1. Do you think the idea is implementable for solving the three pose parameters mentioned above in 2d ?
    2. I understand that chamfer matching is variant to scale changes , so how can i deal with scale changes between the template and the image scene ?

    I look forward to hearing from you. Thanks for your time !

    Reply

    1. The chamfer method looks promising. I would start with a brute force method by trying templates of different rotation and scale. If that works you can look at ways to speed it up later.

      Reply

        1. Never said it was. It’s one of the four methods you can use in conjunction with ICP from Besl and McKay’s paper, and that’s where I got it from.

          Reply

  90. Hi,
    Firstly, thanks for your post. it is very useful.
    I have a problem.I have two set of 4 points.you can see following lines
    A = [0,0,0;
    0,0,1;
    0,1,0;
    0,1,1]
    B = [10,10,10;
    10,10,20;
    10,20,10;
    10,20,20]

    When I run your octave code , I get results like
    Rotation :
    1 0 0
    0 1 0
    0 0 1

    Translation :
    10.000
    14.500
    14.500

    Then, I use A matrix rows as test points
    Results like :
    A[ 0 0 0] => B[10, 14.5, 14.5]
    A[ 0 1 0] => B[10, 15.5, 14.5]

    There is a mistake. Bu I can’t find anything.
    am I getting something wrong?

    Reply

    1. The algorithm doesn’t do scaling. Your A and B have different scaling, the algorithm will fail to give meaningful results.

      Reply

      1. Actually, that only applies to 2D points.

        If your points have a 1:1 mapping then you can undo the scaling of one of the point set. Translate the point to the centroid, shrink them so all the distances to the centroid are similar to the other point set. Then add the scaling back in later.

        Reply
  92. Pingback: Camera pose estimation: How do I interpret rotation and translation matrices? - HTML CODE

  93. Great tutorial, thanks.
    It works great as long as the shapes are similar (low noise).
    Do you know maybe a robust way to superimpose two point-clouds of equal size and fixed assignment but varying shape?

    Reply

    2. I don’t know what you mean by “more robust”. If I understand the method he is using correctly, then it minimizes the RMS error between corresponding points from either point cloud. It can accept any pair of ordered point clouds (of the same size), regardless how similar they are to each other. Think of it this way:

      1) Attach springs (of rest-length 0) to corresponding points from either point cloud. (Note: Each spring has energy (1/2)kr^2. The sum of the energies of the springs is proportional to the RMS error, r^2.)

      2) Allow the springs to relax.

      The resulting rotation and translation of the two point clouds minimizes the energy (and hence minimizes the RMS error). Now it would be straightforward to write a little physics simulation that iteratively relaxes the springs until they don’t move anymore, taking into account the force on each point during each iteration. What’s clever about the algorithm Nghia Ho is using is that it performs the entire minimization in a single step, simply by finding the eigenvectors of a 3×3 matrix.

      If by “more robust” you mean that you want to discard outliers, or use a different cost function (ie. not RMS), then you might have to resort to the simulation approach I mentioned above (perhaps cutting some springs if they get too long, or using springs whose energy is not proportional to the square of the distance). I don’t know if this is the best approach. (This is the first idea that popped into my head.) But it gives your more flexibility for choosing the error function. Be warned that figuring out the best criteria to use to discard outliers is a thorny and contentious topic in statistics, and it is beyond my knowledge.

      I don’t think I answered your question, but hopefully I clarified what (I think) the method does.

      Incidentally, at first glance, the method Nghia Ho is using sounds almost identical to the method described in:
      R. Diamond, (1988) “A Note on the Rotational Superposition Problem”, Acta Cryst. A44, pp. 211-216.

      For what it’s worth, I implemented this method in python here:

      https://github.com/jewettaij/superpose3d

      and in C++ here:

      https://github.com/jewettaij/superpose3d_cpp

      (This version optionally supports scale transformations and inversions. Please excuse the blatant self promotion.)

      Reply

  94. Hi thanks for this very simple explanation.

    I am trying to rotate and transform a set of 7×3 coordinates, A, to align with a set of 3×3 known anchor points, B. When I use the 3×3 sub matrix of A the points line up correctly. How do I extend this rotation to the full matrix A to find the other 4 coordinates transformed?

    It’s been a number of years since I did any matrix theory and I can’t remember how to go about it.

    Reply

    1. There’s no obvious single solution. If your problem is similar to aligning 3d point cloud then each point in A will have a match with points in B, even if they are different size. Example

      A1 -> B1
      A2 -> B3
      A3 -> B2
      A4 -> B2
      A5 -> B1
      A6 -> B3
      A7 -> B3

      Each point A is matched with the nearest point in B.

      Find R, t. Apply to A, then repeat until the error converges.

      Reply

  95. Hi Nghia,
    Thanks a ton for uploading this simple-to-use code. In fact, the problem I am struggling with is a bit different than those of most people on here talk about. I just sent you an email on my question. It is certainly rigid motion analysis of a two-piece machine.
    Please let me know if you get the email.
    Cheers,

    Reply

  96. Hi,
    thanks for the code.
    Are you planning to have a ransac implementation of the algorithm, since sometimes the corresponding between two sets
    of 3d points is not that perfect.

    Reply

  97. I am currently working on KITTI Visual odometry dataset.
    I have generated poses for the sequences but facing difficulty in checking the translational and rotational error.

    There is a development kit which is used for evaluating the estimated poses which can be downloaded from
    http://www.cvlibs.net/datasets/kitti/eval_odometry.php

    I cann’t figure out how to send the poses estimated to the “evalute_odometry.cpp” file available in this development kit.
    It will be a great help if you can tell me how to give parameters to this c++ code .

    Reply

  98. Hi nghiaho,
    Great tute thanks, hoping you’d be able to help or point me in the right direction…
    I have two sets of 3D points which I want to align – set A, set B.
    Set B have a constant offset from A and that offset is unknown.
    I need to find the translation, rotation and offset.
    What would be the best approach using your code?..or other?
    Many thanks

    Reply

    1. Without knowing your dataset I’m going to take a stab and say have a look at iterative closest point (ICP).

      Reply
  101. Pingback: Kabsch algoritm | minusite

  102. Very nice, tutorial. I was curious if you happen to know how can I estimate the derivative (first and second) of the rotational matrix knowing the positions of the two sets with respect to time.

    Reply

    1. This I don’t know but I’ve seen it mentioned in the book “An invitation to 3-D vision” by Yi Ma. You might find it helpful

      Reply

  103. Hey,
    thank you for your work. How to arrange the script for a rotation only? Just leave the calculation of “t”?
    kind regards,
    D.

    Reply

  104. I wonder if you have noticed this paper:
    Uncalibrated stereo visual servoing for manipulators using virtual impedance control
    used your figures and even text.

    Reply

  105. Thanks for the method.
    How about if each dataset includes only two points (not three or more). I know that the solution will not be unique, but any criteria can be assumed to make the solution unique? (e.g. no rotation in a particular axis).
    Thanks.

    Reply

    1. Possible, but you’ll have to figure out the maths formulation specific to your application.

      Reply

  106. The alternative check for the special case resulted in the invalid R for me while the original check worked.

    R should be close to identity as my points were almost same
    R before check was close to (1 0 0, 0 0 -1, 0 -1 0) which is reflection
    R after alternative check was close to (1 0 0, 0 0 1, 0 -1 0) which is now rotation but incorrect one (for this case)
    R after original check was close to identity as expected

    Reply

  107. I’m just wondering if there’s a bug in the Python reflection case. The post says that the 3rd column of R is multiplied by -1, but in the code, it says:
    Vt[2,:] *= -1
    Should this instead be:
    Vt[:,2] *= -1
    since the first index refers to the row and the second to the column?
    In the documentation for numpy.dot, you can see in the example that for the given matrices, the first index refers to the row, and the second to the column.
    http://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html

    Reply

  108. Hello,

    I wonder if you have tried ICP algo for Kinect registration to align cloud A to cloud B. How about your result? Even if I have got a relatively fine fusion result, the far background doesn’t seem to fuse. Anymore, what’s the ICP or SAC-IA parameters you use to register.

    Thanks!
    Zhaokai

    Reply

    1. I’ve only used ICP in the context of laser point cloud registration and it works fine. I have not played with any Kinect data so can’t comment.

      Reply

  109. Hey! great explanation ! just what i was searching for :).I just have a doubt in your python code, from where exactly the variable “T” gets its value(line 59 of code)?Because it suddenly appears at 59th line without any assigning of the value.I am new in python.

    Thank you

    Reply

  110. Hey! i am working on a similar thing.I am having a rotated stl file with respect to x axis, which i am able to run in python and i have its normal stl too,I wanted to make the rotated stl file to its normal, so that they align.But In your python code you have taken a random 3×1 rotation and translation matrix and then computed to minimize rmse.I wish to do the same, but do you know how can i find my rotation and translation matrix?
    Thank you in advance.

    Reply

    1. Find the rotation angle between two vectors and a rotation vector (cross product of two vectors) to rotate around.

      Reply
  111. Pingback: p3p – Hyejun

  112. Dear Nghia Ho,

    I have a question regarding the reference you use for the method you describe:

    A Method for Registration of 3-D Shapes’, by Besl and McKay, 1992

    The previous reference is the ICP method.

    But the method you are using is the SVD version of the orthogonal problem, originally described by:

    P. H. Schonemann. A generalized solution of the orthogonal Procrustes problem. Psychometrika, 31:1-10, 1994.

    The version you are using I believe is found in:

    G. Golub and C. van Loan, Matrix Computations, Johns Hopkins University Press, Baltimore, Maryland, 1983.

    or

    K. S. Arun, T. S. Huang, and S. D. Blostein, Least-squares fitting of two 3-D point sets”, IEEE Trans. Pattern Anal. Mah. Intel l., vol. 9, pp. 698-700, 1987

    Please have a look and see if it makes sense.

    Best regards,
    Filipe

    Reply

    1. I’m struggling to remember where I even got the SVD version from now. I vaguely remember it was a paper describing 4 different methods for solving rigid transform between 3D points, which may have reference Arun et al.

      Reply

      1. I see, in anycase I suppose Arun is the most similar method. I just commented because it was confusing for me to see the icp paper you reference (I believe they are using quaternions).
        But nice site very helpful.

        Best regards
        Filipe

        Reply

      2. Paper title “Estimating 3-D rigid body transformations: a comparison of four major algorithms” from university of new haven

        Reply

  113. Thanks for the code, it works really well. I have one question with this method. How can i add the weight for each point pairs according to different measurement accuracy.

    Reply

      1. just noticed the octave is similar to Matlab, changed few lines and it worked. Now, I need to test my own points

        thanks anyways 🙂

        Reply

  115. Hi,i have the point cloud map data from the kinect and a maker(for define world coordinate system,4 pts of a marker).
    As well,I have 4 3-d pts in could A(from kinect) and 4 3-d pts in cloud B(user-defined).I have calculated the rotation and translation vector using your method.But when i use the rotation and translation matrix to test and verify,i think it runs out wrong.
    Here is the data i used.

    Cloud A(4×3 matrix,each row is a 3-d point’s xyz):
    [0.2198967337608337, 0.07611807435750961, 0.9740000367164612;
    0.3156218230724335, 0.06959863752126694, 0.9320000410079956;
    0.2888424396514893, -0.03973493725061417, 0.8800000548362732;
    0.1901302933692932, -0.03515014424920082, 0.9200000166893005]

    Cloud B(a 4×3 matrix,corresponde with Cloud A’s coordinate in user-define system):
    [0, 0, 0;
    1, 0, 0;
    1, 1, 0;
    0, 1, 0]

    rotation mat:
    [0.9204804047697497, -0.05122804701289122, -0.3874164576191395;
    -0.2262727156590027, -0.8781476223977179, -0.4214942602521828;
    0.3186165133561311, -0.4756389812415292, 0.8199091882277589]

    translation mat:
    [0.6263936656823152;
    0.963452529594535;
    -0.8320317417584704]

    I have use rot_mat and trans_mat to tranform the CloudA’s row[1](the first point in Cloud A,in Cloud B should be ‘0,0,0’)
    ,but the result was ‘0.447561275944713,0.436317567501983,0.000417844947336099’.

    Would you give me some advice ,thank you!

    Best regards,
    DxZhu

    Reply

  116. Dear Nghia Ho,

    The CloudA and CloudB i mentioned before is in different scale. Is this situation suitable for your method?
    (I’m sorry for my poor English…)

    Best regards,
    DxZhu

    Reply

      1. Thank you for your reply.I made a mistake in my research.The 2 coordinate system was in same frame,now i merge them.It works as expect.

        Reply

  117. I have two set of 3d points. One set is of nominal points and the other one is measured one. I have to get the transformation matrix to fit the measured points on the nominal points. But the size of nominal points and the measured points is different. Your function has assertion of both sets of points to be equal. is there a way around that?

    Reply
  118. Pingback: Finding rotation for magnetometer data to astronomical coordinates | w01f359

  119. Hi,
    I wonder if you have come across the problem I face:
    I have 6 points in 3d-space, they are markers on a rigid body which then are tracked by a motion capture system. Sometimes one or more markers are hidden, so the simple calculation of the centroid would result in points that are totally of. How can I compensate this, using the fact that all points are on a rigid body?

    Any help would be greatly appreciated!
    Yours,
    Damian

    Reply

    1. With only 6 points you can probably brute force this. Try finding all possible pairing combinations between observed and model and see which one fits the best.

      Reply

  120. I tried this on these two plots:
    A = [[1 1 0]
    [3 1 0]
    [2 2 0]]
    B = [[ 1 0 0]
    [ 3 0 0]
    [ 2 -1 0]]

    I got a t = [[ 0.2 -0.46666667 0. ]
    [ 2.2 0.86666667 0. ]
    [ 2. -0.33333333 0. ]]

    I expected t = [[ 1 0 0]
    [ 3 0 0]
    [ 2 -1 0]]

    Am I incorrect in that assumption?

    Reply

        1. If the code works then my coordinates_after should equal my new_coordinates_predicted in the code below I believe. Can you see where I went wrong? This code below can be saved as a python file and run as such.

          import numpy as np
          from math import sqrt
          import matplotlib.pyplot as plt
          import numpy as np

          # Input: expects Nx3 matrix of points
          # Returns R,t
          # R = 3×3 rotation matrix
          # t = 3×1 column vector

          coordinates_before_x = [1, 3, 2]
          coordinates_before_y = [1, 1, 2]

          coordinates_after_x = [1, 3, 2]
          coordinates_after_y = [0, 0, -1]

          t = np.arange(3)
          plt.scatter(coordinates_before_x, coordinates_before_y,c=t)
          plt.scatter(coordinates_after_x, coordinates_after_y,c=t)

          coordinates_before = np.column_stack((coordinates_before_x, coordinates_before_y, [0,0,0]))
          coordinates_after = np.column_stack((coordinates_after_x, coordinates_after_y, [0,0,0]))
          print coordinates_before
          print coordinates_after

          def rigid_transform_2D(A, B):
          assert len(A) == len(B)

          N = A.shape[0]; # total points

          centroid_A = np.mean(A, axis=0)
          centroid_B = np.mean(B, axis=0)

          # centre the points
          AA = A – np.tile(centroid_A, (N, 1))
          BB = B – np.tile(centroid_B, (N, 1))

          # dot is matrix multiplication for array
          H = np.transpose(AA) * BB
          print H
          U, S, Vt = np.linalg.svd(H)
          print “u:”,U, “S:”,S, “Vt” ,Vt
          R = np.transpose(Vt) * np.transpose(U)

          # special reflection case
          if np.linalg.det(R) < 0:
          print "Reflection detected"
          Vt[2,:] *= -1
          R = np.transpose(Vt) * np.transpose(U)

          t = -R*np.transpose(centroid_A) + np.transpose(centroid_B)

          return R, t

          R, t = rigid_transform_2D(coordinates_before, coordinates_after)
          print "This is t" , t
          new_coordinates_predicted = (R*coordinates_before) + t

          new_coordinates_predicted = np.transpose(new_coordinates_predicted).tolist()
          new_coordinates_x_predicted = new_coordinates_predicted[0]
          print new_coordinates_x_predicted
          new_coordinates_y_predicted = new_coordinates_predicted[1]
          print new_coordinates_y_predicted
          plt.scatter(new_coordinates_x_predicted, new_coordinates_y_predicted, c = 'red')
          plt.show()

          # Random rotation and translation
          R = np.random.rand(3,3)
          t = np.random.rand(3,1)

          # make R a proper rotation matrix, force orthonormal
          U, S, Vt = np.linalg.svd(R)
          R = U*Vt

          # remove reflection
          if np.linalg.det(R) < 0:
          Vt[2,:] *= -1
          R = U*Vt

          Reply

          1. Check to make sure your input is row major eg. Nx3. It’s easy to mix them up when you only have 3 points because a column major will still work but give the wrong answer.

  121. Hello,
    How this method works if there are two data set with different sizes ?
    Example : A has 30 points and B has 70 points

    Reply

          1. Would I first align my two 3D point set using the known corresponding pairs using your algorithm then apply the TrICP?

            Do you know of any base TrICP code on the web that I can start with?

          2. I am now creating the TrICP algorithm in python. I am would love to compare my code to any other base code but cannot find any online. Do you know of any TrICP base code in python?

          3. No. But the algorithm is not that difficult if you follow it step by step as outlined in the paper.

  124. Hi Nghia,

    Could you please help me with a question I have when I tried your matlab script.
    As I understand, the relationship between A, B, R is B=R*A+T;
    while I found B is not equal to R*A, in which R was obtained exactly the same as you describe in your script. The B= (R*A’+repmat(ret_t,1,n))’ and if there was no translation then the B=A*R’, which is not the way I need. I am so confused and don’t have any idea what went wrong.

    Thanks a lot!

    Best

    Reply

      1. Hi Nghia,

        I am sorry I didn’t make myself clear. I don’t have any background on math while I need to calculate the rotation matrix between a set of points.

        Here is a example to show my problem:
        A is the matrix representing a set of point before rotation.
        B is the that after rotation and R is the rotation matrix.

        if A=
        -0.16678 0.54059 0.82459
        0.75941 -0.46297 0.45712
        0.62887 0.70244 -0.33331

        and if R=
        0.949565 0.134855 0.283092
        0.040814 0.841966 -0.537985
        -0.310904 0.522405 0.793997

        then for B=R*A should be :
        0.12207 0.64975 0.75029
        0.29426 -0.74564 0.59785
        0.94790 0.14780 -0.28222

        If A and B are known, then I use your program to try to get R,
        [ret_R,ret_t]=rigid_transform_3D(A,B)
        Reflection detected
        ret_t =
        9.4872e-08
        6.2863e-08
        -8.0264e-08

        ret_R =
        0.799215 0.595592 -0.080776
        -0.581664 0.800281 0.145662
        0.151399 -0.069431 0.986031

        Here is my problem: the ret_R != R, and ret_R * A != B
        ret_R * A=
        0.268206 0.099565 0.958203
        0.796354 -0.582631 -0.162364
        0.542113 0.806615 -0.235554

        But I found that A * ret_R’ = B.

        I don’t know where I made mistake or I understand anything wrong. I Could you please have a look? Thank you very much!

        Best

        Reply

        1. A common mistake is mixing up row and column major for points in a 3×3 matrix. If you can add a 4th point and re-run the code it will eliminate any ambiguity,

          Reply

          1. Hi Nghia,
            Thanks for your suggestion! Really help! I thought about the row column things before but still mistakenly thought R*A’=B. Your suggestion is great and I never thought about adding another point since I only work on 3 points. Thanks and have a great weekend!

            Best

  125. Hello,
    thanks for your script. I tried to use it, but my input data still is a .xyz file and I’m a python newbie. I only get 1×3 matrices but can’t append my matrices into 3×3 with the xyz values. For your script, I need 3×3 input matrices with the datatype float64. Am I thinking too difficult, is this .xyz to 3×3 matrix easy for one who knows python better?
    My input looks like this for example:
    15.486586, 46.798954, -6.232800, 15.445764, 46.807576, -6.249205, -0.040822, 0.008622, -0.016405, 0.044832;
    6.233575, 48.083754, -4.223557, 6.187027, 48.090785, -4.243389, -0.046548, 0.007031, -0.019832, 0.051083;
    -2.159452, 40.818712, -3.104244, -2.200572, 40.818489, -3.120266, -0.041120, -0.000223, -0.016022, 0.044132;
    45.554111, 131.689322, 1.525740, 45.452954, 131.721406, 1.483290, -0.101157, 0.032084, -0.042450, 0.114298;
    28.315109, 146.107918, 2.897549, 28.235633, 146.131800, 2.864060, -0.079476, 0.023882, -0.033489, 0.089489;
    7.303209, 138.223347, 4.702106, 7.250850, 138.242379, 4.679564, -0.052359, 0.019032, -0.022542, 0.060098;
    -32.211983, 148.909744, 12.919538, -32.279077, 148.907541, 12.876267, -0.067095, -0.002203, -0.043271, 0.079868;
    -48.926024, 180.295215, 20.142896, -49.008547, 180.275117, 20.127614, -0.082523, -0.020098, -0.015282, 0.086299;

    but I only need the first three columns which contain the xyz data and this in one matrix with datatype float64. I only get a matrix 1×9, (nine values horizonzal, not three columns vertical).
    Did you experience something similar? Or did you always use random values?
    I hope somebody can help me, tried everything from stackoverflow all day.

    Reply

    1. I’m not a python expert but I believe you want to do

      1. Treat the .xyz file as a CSV and load it into a numpy array
      2. Grab the first 3 columns from the array using Python’s matrix block selection

      Reply

  126. Hi there!

    Thanks a lot for this great post, it helped me a lot.

    If anyone wants to implement this with OpenCV, be aware that its SVD function returns the matrices in a different order and V is transposed.

    A few remark on the special reflection case:
    1) The text says “determinant of V”, but the code computes the determinant of R (which is correct, so the text is wrong).
    2) The “<" operator is displayed as "<", which might confuse people.
    3) The supposedly easier check suggested by Nick Lambert doesn't work for me (gives wrong R), while the other one does. Negating the third column of R is not the same as negating the third column of V and then recomputing R. You get different matrices! So you might want to remove that. I did tests using randomly generated points and verified R and t by looking at the error.

    Best regards,
    David

    Reply

  127. Hi,
    Thanks for tutorial,
    I have few questions. You said H matrix should end up in 3*3 matrix. How can it be possible if my correspondence are more than 3. Is it possible to register point clouds having overlapping view? i mean suppose i have two kinect sensors having overlapping view. Can i use your tutorial in that case ? Especially Kinect sensor gives lot of noise. Can u suggest me how to overcome that noise during registration process ?
    Thanks in advance,

    Reply

  128. Dear Nghia Ho,

    I’m a PhD student and I’m trying to apply this method to two Kinect Datasets. I’m recording a person walking around with two faced Kinects. So at first the person is backwards to the camera 1 and frontwards to camera 2. What I’m trying to do is rotate the skeletons points of camera 1 like it was camera 2 so, once I represent it both of them should look almost the same.

    I can’t see if this could be done with this method, because I have tried with dummy points (a triangle see from front and side) and it works perfectly, but with the kinect datasets the result file from rotating A to B is like a A’ just translated.

    I’m using three points (hip left, hip right, head) from one frame of each file where the person is in the same position due that both files are recorded at the same time (so same position, different views)

    Any advice? I have done an R implementation, but I have checked that same R and t are being generated.

    Thanks in advance.

    Reply

  130. I know this is an old thread, but in case someone’s still reading this: very nice method. I agree with some of the above comments that in Python the “*” operator should be replaced by “.dot()” (i.e. A*B in Matlab corresponds to A.dot(B) in numpy; reading the documentation of Matlab and numpy confirms this).

    I like it a lot that this method generalizes to any dimension without changing anything but the number “3” to a symbol “K” indicating the dimension.

    One remark that no-one has yet made, though: I expected this method to be completely general, but it doesn’t work if A and B are rank-deficient, meaning that the vectors in A are expressed as K-dimensional tuples but are all, in fact, in a proper H-dimensional subspace of \mathbb{R}^K. I am using the following (Python) example:

    n = 3
    A = zeros((n,n))
    A[0] = [0,0,0]
    A[1] = [1.22664, 0.0, 0.0]
    A[2] = [-0.77977173025500601, -1.1568922037921743, 0.0]
    B = zeros((n,n))
    B[0] = [-0.77 , 0.49 , 0. ]
    B[1] = [-1.33 ,-0.6 , 0. ]
    B[2] = [ 0.62 , 0.66 , 0. ]

    Whereas A and B are very slightly off, the matrix (A’ = R . A + t) is not a congruence of A, as the following Euclidean distances show:
    ||A0-A1|| = 1.227; ||B0-B1|| = 1.225; ||A’0-A’1|| = 1.452
    ||A0-A2|| = 1.395; ||B0-B2|| = 1.400; ||A’0-A’2|| = 2.471
    ||A1-A2|| = 2.316; ||B1-B2|| = 2.322; ||A’1-A’2|| = 1.715

    I’m rather surprised because, tracing through the code execution, the rotation matrix is correctly (?) identified as decomposed into an upper-left 2×2 block and a lower-right 1×1 block. But the result is obviously wrong.

    My next port of call will be to project A,B on the subspace and work in full dimension (i.e. 3 vectors in 2D). But it would be nice to have a completely general method that works in any dimension and that also holds in rank-deficient cases.

    Reply

  131. Thanks a lot for this! I managed to do this purely with PHP by converting the python code. The result is identical. But the SVD from here: https://github.com/d3veloper/SVD
    has shifted 2nd and 3rd columns for V and U compared to numpy SVD. That means with the special reflection case you have to multiply the 2nd column of V with -1, not the 3rd. That took me some time to find out..

    Reply

  132. Hi,
    Your blog is very useful.
    It helps me to solve ICP problem while using PCL library.
    We need to apply translation after using PCL library.
    Thank you so much.

    Reply

  133. Dear Nghia Ho,

    I have been using this code and it works wonders, however, I am using it to plot change in Euler angles and I am obtaining an odd creep in my data. I am wondering if my matlab function for obtaining the rotation matrix or my function for decomposing the rotation matrix are slightly wrong.

    function [R,t] = rigid_transform_3D(A, B)
    if nargin ~= 2 %input check
    error(‘Missing parameters’);
    end

    centroid_A = mean(A);
    centroid_B = mean(B);

    N = size(A,1);

    H = (A – repmat(centroid_A, N, 1))’ * (B – repmat(centroid_B, N, 1));

    [U,S,V] = svd(H);

    R = V*U’;

    if det(R) < 0
    disp('Reflection detected');
    V(:,3) = -1*V(:,3);
    R = V*U';
    end

    t = -R*centroid_A' + centroid_B'
    end
    %%%%%%%%%%%%%%%%%

    function result = DecomposeR(cloud)
    if cloud(2,1) -1
    thetaZ = asin(cloud(2,1));
    thetaY = atan2(-cloud(3,1), cloud(1,1));
    thetaX = atan2(-cloud(2,3), cloud(2,2));
    else
    thetaZ = -pi/2;
    thetaY = -atan2(cloud(3,2), cloud(3,3));
    thetaX = 0;
    end
    else
    thetaZ = pi/2;
    thetaY = atan2(cloud(3,2), cloud(3,3));
    thetaX = 0;

    end
    thetaZ = rad2deg(thetaZ);
    thetaY = rad2deg(thetaY);
    thetaX = rad2deg(thetaX);
    result = [thetaY, thetaZ, thetaX];
    end

    I know its hard to debug without seeing the entirety of my code but I was wondering if you noticed any errors in how I am calculating R?

    Thank you in advance

    Reply

  134. Hi nghiaho12, your blog is super useful, thank you!
    I actually have a question:
    I am calibrating a 3d laser scanner mounted on a robot arm, what I do is
    1. Scan an object with the laser, it scans from a position pStart to a position pEnd parallel to the ground and gives me a point cloud
    2. Take 3 points from the point cloud and get the correspondent points with the robot arm, so I have the (x,y,z) of the point in the 3d point cloud and the (x,y,z) of the object in the real world expressed according to the robot coordinate system
    3. I’m trying to find a matrix to transform the points from the scene 3d to the points in the robot coordinate system.

    I tried your script, and the idea looks fine to me, but when I take a point P1 taken in the point cloud and I compute:
    P1_Robot = R*P1 + t
    The point obtained is not correct, if I go in those coordinate with the robot, the point is not the same that I’ve seen in the point cloud.

    I’ve tried to take a 4th point but the R that I obtain is now 4×4, so how can I transform a (x,y,z) point using the 4×4 matrix?

    It’s one of my first approaches to this and I’m stuck.
    Thank you for your help 🙂

    Reply

    1. I think it’s sort of working. The only problem I have now is that the robot may scan the 3D object from a different pose with a different rotation.
      Do you have any idea on how to include this rotation?
      I know the robot is scanning in (x°, y°, z°) and I can compute the rotation matrix with eul2rotm, can I compose this with the previous R?

      Reply

        1. Actually not 🙁
          The camera is moving. So if I use your method, it’s fine for the 3D scan in that specific scanning pose. But as soon as I scan from another pose, it does not work anymore.
          I have the pose of the camera w.r.t to the robot base, and I should, somehow, include this in the equation, in order to obtain a single homogeneous matrix to trasform the points in the points cloud to their relative point in the real world in robot base coordinates.
          I don’t know how to do that even after many tried

          Reply

  135. Assuming I have the Rotation and translation Matrix R and t, and Point sets A and B. I have a different set of points C that were relative to coordinate system B, and taken in the same image as point set B. When I calculate NewC=C*R+t I get incorrect values for original points; I am using NewA=A*R+t to check. It seems the centroid was correctly transformed to coordinate system B, but rotation is incorrect. The points should all lie on the same plane in my case. Is there something I am missing?
    A=[ -17.73010 -2.30848 118.89200;
    -21.63380 -2.26028 119.78000;
    -17.70150 1.69298 118.83400;
    -21.60660 1.74509 119.71900]

    B=[-8.536356, -13.781024 ,-1.960194;
    -12.527737, -14.089939 ,-1.960093;
    -12.831648, -10.098786, -1.960194;
    -8.841435, -9.791192, -1.960093 ];

    C=[ 4.21149 , -2.68912 , 113.97200;
    4.20038 , 1.33175 , 113.93800;
    0.29096 , 1.33141, 114.82100;
    0.29096 , 1.33141, 114.82100]

    R= [ -0.0700063 -0.0899049 -0.9934869;
    0.0018309 0.9959171 -0.0902538;
    -0.9975449 0.0081373 0.0695559]

    t=[ 106.98678;
    -0.81361;
    23.54685]

    Any help would be greatly appreciated.

    Reply

      1. Thank you for your response. It turns out my points were in the wrong order when applying the transformation and rotation matrix. Works perfectly now.

        Reply

  136. greetings nghia ho
    very thankful to you, I am working on stereo VO, I am using your python code for finding “R” n “t” values but, I am facing a issue I am getting translation 3×3 instead of 3×1, not getting what went wrong, will you please help me?

    thanks

    Reply

  139. Hi,

    Thank You very Much for the great help on this tutorial. I’ve coded in C++ using opencv. I worked with 63 feature points and I got the rotational matrix size 63 by 63, when the result is computed.

    And I didn’t get the idea to minimize it to 3 by 3, typical rotational matrix. Appreciate if you can assist me on this.

    Thank You

    Reply

  140. Hey,

    Thanks a lot for the very simple code. I am architect and I used it to fit a prefabricated façade to a not so well build structural concrete skeleton. Unfortunately I found your code not at first sight so for the first building I had to solve the problem by trial and error. I wrote a little python app and I want to implement a switch to leave out rotation and just use translation. For that purpose would I just calculate the distance between centroid_A and centroid_B?

    Thanks in advance,

    Paul

    Reply

  141. Hey Nghia,

    I tried your Matlab code, it works with only two points as well as with three points. In fact, the rotation matrix has three degrees of liberty (three angles around the original axis) and the translation matrix has 3 degrees of liberty, so it may work with two points (6 equations and 6 unknowns), can you confirm it?

    Reply

    1. Late reply. Two points will always leave at least 1 degree of freedom in 3D. Two points make a line, that you can spin around.

      Reply

  142. Hi Nghia,

    I’d like to make a rotation about a single axis and perform the rest of the transform through translation for a 3D space. Do you know any way I could modify the matlab code to go through this? I understand that it’s not finding the optimal positioning but I’d like to place the constrains on the object that is represented by the data points.

    Thanks!

    Reply

  143. Also, if I wanted to move my part from its origin (let’s call this P), with respect to an inertial reference frame origin (let’s call this O), I’m assuming I would have to find the change in distance from O to centroid_A and O to P. Is that correct?

    If so, how would that affect the rotation since the rotation would not be around centroid_A but instead around P?

    Reply

    1. If it’s a numeric problem then plug in the numbers to see the change in rotation and translation. If it’s algebraic then start with RA + t = B and introduce your transform on A with matrix algebra,

      Reply

  144. February, 28th, 2018

    Perfect !!
    Your short program solved my problem, but what I really know to appreciate is your explanation, nicely written easy to understand.
    Congratulations !!

    Reply

  145. This is very useful code. I tested in Matlab, and there are few corrections are required. Then it works as expected.

    My question is that how to extract the 3D rotation values instead of matrix?

    Reply

  146. How is the script exactly executed in matlab please?
    I have created two 5×3 column vectors. One with 5 points with respect to coordinate axis 1 and the other with the same 5 points but with respect to coordinate axis 2.

    If correct, how should I proceed please?

    The code you’ve provided should provide the transform matrix that translates and rotates the points from axis 1 to axis 2. Can you confirm please?

    Reply

  147. Hello,

    id like to transform the code in excel or VBA, can someone help me.

    Its a common problem in a survey jobs to change between two coordinate systems, and i’d like to do it with a pair of point clouds on excel, im lost, can someone help me ?

    many thanks

    Reply

  148. Hi nghiaho,
    Thanks for this tutorial. I had two cameras at different angles viewing the same 3D points. May i know how would I go about finding correct rotation and translation?
    I tried using your python code but i am getting to high RMSE: 41.9542558078.
    This is my points and final results
    Points A
    [[ 130 33 2161]
    [ 139 94 2157]
    [ 149 153 2249]
    [ 184 83 2218]
    [ 199 47 2225]
    [ 206 112 2252]
    [ 270 118 2273]
    [ 260 23 2271]]

    Points B
    [[ 147 335 2044]
    [ 138 395 2064]
    [ 132 457 2280]
    [ 183 405 2129]
    [ 204 373 2163]
    [ 200 439 2195]
    [ 264 460 2202]
    [ 264 364 2249]]

    Rotation
    [[ 0.49010312 0.86932422 -0.06383052]
    [-0.29881425 0.23635164 0.92457987]
    [ 0.81884613 -0.43406601 0.37560314]]

    Translation
    [[0.54625172]
    [0.67229634]
    [0.53754272]]

    RMSE: 41.9542558078
    If RMSE is near zero, the function is correct!
    May i know what is going wrong??

    Reply

      1. Hi Nghlaho,
        I have checked the point orders by drawing in left and right images, all points are in correct position. As i know only minimal level of python thus i am not really sure how to plot the points in 3D. But i have done some experiment with depth value(z-value), when i am keeping all z-values 0 its giving me RMSE: 1.09521317623. Do you think z value is causing??

        Reply

    2. This is because there is an S(scale) relationship between the two sets of points, which does not support scaling

      Reply

    1. There’s a handful of euler angle representations you can choose from to decompose the rotation matrix.

      Reply

  150. hello, many thanks for your algorithm.
    but now I have a question, in my program I use the function for 3 times, and there is a reflection detected. Does it means my result make no sense? or how can i transform reflection matrix to rotation matrix?
    by the way, in the end, there is 90 degree deviation in yaw angle, roll, pitch, delta , delta Y, delta Z are correct.
    thanks!

    Reply

  152. Thank you for the detailed explanation. Is my understanding correct that the SVD code above only computes the rotation and translation, but not scaling?

    Reply

  153. Thank you for the detailed explanation. The example above demonstrated the rotation and translation of Dataset A to Dataset B based on equation below. Is it correct that there is no effect of scaling demonstrated by the example? How do we add in the effect of scaling into the calculation? Thanks
    B = R*A + t

    Reply

  155. Thanks for you tutorial. I reimplemented the code by C++ to solve 2D image registration, and the code works very well while the objects in two images on the same scale.
    However,I want to solve the scaling transform between images and looked up for some literature. It mentioned a isotropic scale iterative closet point method”Robust isotropic scaling ICP algorithm with bidirectional distance and bounded rotation angle”.
    The result seems very well. I wonder solve the scale problem based on your code and the method mentioned above. While the problem is that “How can I add the scale factor into the code while solving the R t transformation?”Whether SVD can still be used in the solving process?
    I would really appreciated if you could help me , I’ve been fighting with it for days o(╥﹏╥)o

    Reply

  156. hi, thanks a lot!
    I adjusted your python code for python 3.5, please see below:

    import numpy as np
    from math import sqrt

    def rigid_transform_3D(A, B):
    “””
    fit a rigid transform to a set of 3D points
    Input: expects two Nx3 matrices of points
    Returns:
    R: 3×3 rotation matrix
    t: 3×1 translation column vector
    rmse: root mean square error, 0 for perfect fit
    “””
    assert len(A) == len(B)

    N = A.shape[0]; # total points

    centroid_A = np.mean(A, axis=0)
    centroid_B = np.mean(B, axis=0)

    # centre the points
    AA = A – np.tile(centroid_A, (N, 1))
    BB = B – np.tile(centroid_B, (N, 1))

    # dot is matrix multiplication for array
    H = np.transpose(AA) * BB

    U, S, Vt = np.linalg.svd(H)

    R = Vt.T * U.T

    # special reflection case
    if np.linalg.det(R) < 0:
    print("Reflection detected")
    Vt[2,:] *= -1
    R = Vt.T * U.T

    t = -R*centroid_A.T + centroid_B.T

    # Find the error
    A2 = (R*A.T) + np.tile(t, (1, n))
    A2 = A2.T

    err = A2 – B
    err = np.multiply(err, err)
    err = np.sum(err)
    rmse = sqrt(err/n);

    return R, t, rmse

    if __name__ == "__main__":
    # Test with random data

    # Random rotation and translation
    t = np.mat(np.random.rand(3,1))
    R = np.mat(np.random.rand(3,3))

    # make R a proper rotation matrix, force orthonormal
    U, S, Vt = np.linalg.svd(R)
    R = U*Vt

    # remove reflection
    if np.linalg.det(R) < 0:
    Vt[2,:] *= -1
    R = U*Vt

    # number of points
    n = 100

    noise = np.mat(np.random.rand(n,3))*0.001

    A = np.mat(np.random.rand(n,3));
    B = R*A.T + np.tile(t, (1, n))
    B = B.T + noise; # transpose and add some noise

    # recover the transformation
    ret_R, ret_t, ret_rmse = rigid_transform_3D(A, B)

    print("Points A")
    print(A)

    print("Points B")
    print(B)

    print("Rotation")
    print(R)

    print("Rotation fit")
    print(ret_R)

    print("Translation")
    print(t)
    print("Translation fit")
    print(ret_t)

    print("RMSE: {}".format(ret_rmse))

    Reply

    1. Hi Mark,

      Can you please offer an example of the data entry required for your Python script, is there a limit on the maximum number of corresponding pairs of points that can be used ?

      Reply

  157. Hello, can I use the python script in my codes with modifications for research purposes with credits to you?
    Thank you!

    Reply

  158. Hello Nghia Ho,

    Your little article here has probably generated more interest and comments than you ever thought it would. Like others, I am interested in the “reflection” case. I put your original Python code in a loop running 100000 times and set up a variable to count the number of refection results obtained. I was surprised that the random matrix creation created data for a reflection case exactly ZERO times. I was wondering if you ever saw it encounter a reflection case, because if not I’m wondering how you verified the logic of that section of code.

    Reply

    1. I have seen it on rare occasions during my PhD when using it with ICP to align point clouds. I worked around it by using more points (instead of the minimum of 3). But yeah, I have not put anytime into verifying the solutions provided by other people.

      Reply

  159. Isnt there a far simpler solution by simply using least squares.

    Let :
    A := nx4 matrix where each point from PA is in each row with 1 in the last coordinate

    B:= nx3 matrix with each point from PB in each row.

    Then we are seeking a linear transformation M (3×4 matrix) from traspose of A (At) to transpose of B (Bt)

    Thus M * At = Bt

    => M * At * A = Bt A

    => M = Bt * A * Inverse( At *A)

    M can be decomposed into a translation and decompose the inner 3×3 of M to get the rotation and scaling of M .

    Reply

  160. Hi,

    Thank you so much for this good tutorial. I’m trying to build a script that let a robot pick up a cube that is detected on a camera. It has been a bumpy ride.. But I’m almost there.

    I have some questions:
    – Can I map u,v pixel values to robot coordinates x,y with your solution?
    – Is your solution also suitable for solving x,y and z values?
    – Is your solution the same as finding the homography matrix, as desribed here: https://www.learnopencv.com/homography-examples-using-opencv-python-c/
    – If yes, should I use that approach instead of yours?

    I’m not experienced yet on the subject, so sorry in advance if the questions are stupid 😛

    Reply

    1. What I present here is not applicable to your problem. You want 3D pose estimation from 2D homography. Look up OpenCV’s solvePnP function.

      Reply

  161. Excellent tutorial!

    I implemented this in C# using Math.Net numerics and it works flawlessly. Of note, I tried using

    if determinant(R) < 0
    multiply 3rd column of R by -1
    end if

    And it regularly misaligned everything by 180 degrees. Your first suggestion to recompute R worked in 100% of cases

    if determinant(R) < 0
    multiply 3rd column of V by -1
    recompute R
    end if

    The reflection case comes up very often for me as I’m running this over just 4-8 points.

    Reply

  162. Hi there

    I have a problem where there is some noise in my dataset. Therefore the “optimal” rotation found by this solution may not be realistic. Is there a way to limit rotation (say in 2d case between +/- 45 degrees) and determine a “sub-optimal” but more realistic solution?

    Many thanks

    Reply

  163. Hi,

    I’ve built an interative closest point algorithm/utility for Blender (a while ago) and for a while I just had some simple comments and links in the code for citation. It has been used by a lot of people for a lot of different things and it needs to be properly cited. I’ve made a DOI link for my repo via zenodo. Do you have a preference or particular way you would like this cited.
    https://github.com/patmo141/object_alignment
    https://zenodo.org/record/3382818#.XWqGLyhKiUk

    Reply

    1. Hi! Is is possible to perform this algorithm without rotating the input data? or limit which axes of rotation are used? For example, just skip that step and use only XYZ translation? My real word example does not have ability to rotate about certain axes and translation is the only practical way to move to move the points.

      Reply

  165. Hi,

    Thanks for the tutorial.

    My question is if we have an unknown offset in x,y and z (the corresponding points, lets say data set B+ (x,y,z)), then is it possible to simultaneously find unknown x,y,z and optimal rotation and translation between two data sets A and B ?

    Thanks!

    Reply

  166. Some questions:

    1) How would your solution change if random noise was added to the 3D source points?
    2) How would your solution change if the number of points was over one hundred million?
    3) How would your solution change if the correspondences were not known?

    Thanks!

    Reply

    1. 1) no change if noise is Gaussian
      2) no change to algorithm, making it work with limited CPU/RAM is a different story
      3) depends on the use case

      Reply

  167. Hi, I’m trying to match two sets of 3D points and find the transformation matrix. I tried the code you shared, but doesn’t work for my example.
    I couldn’t fix the error “Matrix dimensions must agree.”

    Reply

    1. Probably a simple mistake in transpose. Put a bunch of print out for the matrix size at each step of your program.

      Reply

  169. Hi,
    Great explanation!!!
    Can you please explain why you require a minimum of 3 corresponding points, while MATLAB allow to calculate ‘similarity’ transformation (translation, rotation and isotropic scaling) with 2 pairs of points only? What do they assume in MATLAB function to use only 2 pairs?

    Reply

  170. Am I correct that your solution fails when you have only 3 points.

    Above you reference a solution for 3 points (page_id =57) but I don’t think the link is correct.

    Any comments?

    Reply

    1. My first advice is to get rid of any use of C++ auto with Eigen due to unexpected behavior. This is documented on their website.

      Reply

      1. Yes I’m aware of the potential issues of using auto with eigen types but I was only using it in a few places that did not invovle expression templates. In any case I’ve pushed an update replacing all uses of auto with Eigen types, and I’ve added a rand seed as Eigen doesn’t do this. Still the same results as before.

        Reply

        1. Code works when I make these changes

          Eigen::MatrixXf V = svd.matrixV();
          Eigen::Matrix3f R = V * U.transpose();

          // special reflection case
          if (R.determinant() < 0.0f) { V.col(2) *= -1.0f; R = V * U.transpose(); }

          Reply

          1. Great! thank you for looking into this for me. I assume that in the test code when refleciton is removed from the test rotation matrix it should also be multiplying the coloumn-2 vector and not the row-vector like the other one? oddly enough it seems to work in either case but I know that can’t be right.

    2. Great code, I’ve tried to compile your rigid_transform_3D.cpp code with Eigen 3.4.0 and gcc but I got the follwoing error. I’m now to Eigen – is this maybe a problem with auto?

      rigid_transform_3D.cpp:80:13: error: expected unqualified-id before ‘[‘ token
      const auto [ret_R, ret_t] = rigid_transform_3D(A, B);

      Reply

  172. Hi,
    I am trying to use ICP . it works well for small translations but with large translations im getting an extra rotation matrix computed. Please help.

    Reply
  173. Pingback: Given the coordinates of the same group of points in different coordinate systems, how to solve the conversion relationship between two coordinate systems – Newbie tutorials

  174. I just want to say that the method was first published in 1976, “A solution for the best rotation to relate two sets of vectors”. This is a well-known algorithm (Kabsch algorithm) in the field of crystallography, molecular dynamics simulation, et al…

    Reply

  176. Hello all,

    nghiaho12,Could you please help me if I upload my question regarding the SCD based ICP c++ code?

    Reply

  177. Hi ! How can I cite this for a paper? This looks great, and I’ using it for my research.

    Reply

  178. Hello,

    I’m trying to minimize the displacement (d) between the points along a set of displacement vectors (v).
    Can SVD help me minimize this sort of vectorized least squares regression: Σ||d•v||^2
    or is another method required to do something like this?

    Thanks!

    Reply

    1. I can’t visualize your problem in my head. But if it’s non-linear in nature have a look at Ceres Solver or similar.

      Reply

  180. Hi nghiaho12,
    Context: In my case I have a .pcd image (from a camera) – its a human image, when I do a 3D modelling visualization using PyTorch3D I see that the image is not upright. So in order to rotate and make it upright, what do I have to do? Please point me with some sample code. Basically my points and colors are as follows:
    xyz [[-0.5999598 -0.5431006 1.2567867 ] [-0.53238 -0.49774736 1.1485529 ] [-0.56934434 -0.5381967 1.2408999 ] … [ 0.9114153 0.82416993 1.9144264 ] [ 0.84487355 0.75600845 1.7579422 ] [ 0.90972435 0.80561376 1.8753963 ]]
    rgb [[0.57254902 0.28627451 0.14509804] [0.57254902 0.28627451 0.14509804] [0.07058824 0.28627451 0.14509804] … [0.07058824 0.28627451 0.14509804] [0.85882353 0.42745098 0.71764706] [0.07058824 0.28627451 0.14509804]]

    How do I flip it upright and carry the corresponding color as well? Please respond. Any help is appreciated.
    I am unable to paste my screen shot of the visualization here.

    TIA
    Pankaja

    Reply

  181. Is this really finding the least square solution?.

    Lets say that there is no rotations and only translations. In this case we are only left with step 3 – without rotations.
    Then least square is not found by averaging. ?

    Or am I missing something here?

    Reply

      1. First I’ll preface that I might be missing something.

        But it seems to me that if you have no rotations, then you just set the translation as equal to the difference between the two centroids, which would not be the least square solution?

        Reply

        1. This would still be least squares, assuming Gaussian noise. Here’s one way to look at it. Let’s say you have two datasets A and B, that are related by a translation T only. The measurements have noise Gaussian noise with mean=0 and stddev=1. The aim is to estimate T. In 3D, A, B and N (noise) would be dimensions Nx3, T would be 3×1.

          B = (A + N(0,1)) + T

          Re-arranging:
          B – (A + N(0,1)) = T

          Apply mean to the left side to estimate T:
          mean(B – (A + N(0,1)) = T

          Expanding out:
          mean(B) – mean(A) – mean(N(0,1)) = T

          mean(N(0,1)) approaches 0 for large samples, so we get
          mean(B) – mean(A) = T

          Which is the difference in centroid, and the optimal solution assuming gaussian noise. This in turns minimizes the least squares error stated under “Solution overview”.

          Reply

  182. Thanks for the tutorial, Very very helpful!!

    Though I have a question. I have calculated the rotation matrix(R) and translation matrix(t). Now I want to calculate Homogeneous transformation. What is homogenous transformation and how can I calculate it?

    Thanks

    Reply

    1. Do you mean the 4×4 homogeneous matrix like below?
      |r0 r1 r2 t0|
      |r3 r4 r5 t1|
      |r6 r7 r8 r2|
      |0 0 0 1 |

      where r is your 3×3 rotation matrix and t the translation vector.

      Reply

  183. Hi , thank for a great tutorial. I had some difficulties in using the python code. I have this 2 sets of 9 point data ,

    A = ([9.78, 2.16, 0],
    [9.92, 0, 0],
    [9.81, -1.97, 0],
    [18.97, 4.02, 0],
    [19.02, 0, 0],
    [19.01, -3.97, 0],
    [27.98, 6.01, 0],
    [28.10, 0, 0],
    [28.01, -6.0, 0])

    B = ([9.80, 2.30, 0.02],
    [9.91, 0.30, 0.01],
    [9.83, -1.94, 0.0],
    [18.71, 4.09, 0.01],
    [18.58, 0.21, 0.03],
    [18.84, -3.56, 0.01],
    [27.87, 6.02, 0.03],
    [27.87, 0.25, 0.01],
    [28.47, -5.56, 0.01])

    When I try to run the code, it will return 9 3×3 rotation and 9 translation. When I tried to define R and t to 3×3 and 3×1 in rigid_3D_transform , it returns ValueError . Any idea where I may have gone wrong ? TIA

    Reply

  184. Apologize for such an easy question as I am still a beginner in python and numpy world … Can you point it out specifically where I need to fix …. thanks

    Reply

    1. A = np.array([…],[…],…..,[…])

      If the function complains about incorrect dimensions you might need to transpose A

      A = np.transpose(A)

      Reply

      1. Owh you are awesome ! … My code works now thanks to you ….

        Well, I still got RMSE = 0.281555… but I think that will be my job to find out why…

        Anyway, Appreciate you help much again for this tutorial …:)

        Reply

  185. Hello,
    i want to calibrate the lidar and camera and find the rotation and translation i.e 3d lidar point and 2d camera image ..

    can i use this methód .. what should i change in this one if it so ?

    Thanks in advance.. !!

    Reply

    1. I wouldn’t use this for your task. Yours is more 3D to 2D calibration. Detect the same points in the lidar and image, find a transformation and projection that brings the 3d lidar points into the image.

      Reply

  187. Hi,
    Could you check the following point set, the RMSE is about 0.083086 from your code, I can’t figure out where the problem is.
    A = np.array([[0, 83.68, 72.415, 5.055],
    [0, 4.5, -35.345, -31.47],
    [0, 0, 0, 0]])
    B = np.array([[-100.753, -16.9168, -28.0889, -95.5639],
    [-120.739, -125.344, -85.5882, -89.2883],
    [0, 0, 0, 0]])
    Thanks for your time

    Reply

  188. This is amazing.
    Well written and explained excellent.
    Here’s a question. Because data (points cloud) come from a scan, some portion of dataset A was removed in dataset B and some portion of dataset B was added, meaning the scanner did not “see” objects in B that were seen in A and did see new objects in B that were not seen in A.
    So if the “removed” points and the “added” points, were removed both from the dataset, the statistics would have been much better, meaning the average distance between corresponding points was smaller.
    How can we find those points from both datatset that we better off without them?
    It is reasonable to think that the points are clustered because the scanner moved between A and B so areas of its field of view were exposed to new objects that were scanned?

    Reply

    1. After a lot of reading and searching, I would to answer my own question.
      “The solution presented will work with both noise free and noisy data” says @nghiaho but that depends on what kind of noise.
      If the noise is random, meaning uniformly distributed, then because this solution is based on mean (average) that it’ll work great.

      Random noise is very typical to Lidar sensors.

      But as I mentioned in my question, dataset A and dataset B, each contains some points that were “removed” and points that were “added” because the scanner moved and changed its position and can now “see” new stuff and cannot “see” anymore other stuff. let’s call these stuff “the difference”.

      All over I see the “ICP” algorithm which applies the above algorithm over and over again trying to drop some points from each dataset to reduce the “difference” . But this doesn’t make sense, because there are too many options and this process can take forever.

      My question is, is it true mathematically, that if in addition to dataset A and dataset B, we had dataset C which was taken between A and B, so assuming the change (the rotation and translation) is happening graduately, meanin the scanner moves from point A to point C and then to point B, then if we applied the above algorithm twice, once from A to C and then from C to B, then we reduce the “difference” ?
      Or, because we perform it twice, then we might even get a greater error ?

      Reply

  189. Hi,
    Your implementation is the easiest to understand, thanks so much for your explanations and dedication helping people out!
    I managed to get your implementation working, now I am digging around because I want to understand the scaling aspect of all this.
    I want a check in my code to verify that the scaling obtained is 1, and that the datasets can really be explained with just rotation and translation.
    So I found implementations (https://zpl.fi/aligning-point-patterns-with-kabsch-umeyama-algorithm/ for example) of Umeyame’s algorithm which I thought was going to provide me just this (as an extension of Kabsch’s algo), but how come we absolutely do not get similar answers? It looks like even in his paper Umeyama gives an example where his algorithms rotates and scales wrongly….Do you know anything about this?
    I am trying to do the HEA between a robot held line scanner (3D camera coordinates) and a robot and wondering how in practice this whole will work with uncertainties from the real world coordinates I will be using.
    Thanks

    Reply

  190. Hello, I’m curious about the special case with SVD(R):
    “`
    if determinant(R) < 0
    [U,S,V] = svd(R)
    multiply 3rd column of V by -1
    R = V * transpose(U)
    end if
    “`
    Did you mean?
    “`
    // V1 is from [U1, S1, V1] = svd(h), not from svd(R)
    V2 = V1;
    V2(:,3) = -V1(:,3)
    R3 = V1 * U1'
    “`
    I try with the test case (link is below), it returns the reflection matrix but the `R = V * transpose(U)` before going to the special case (det(R) = -1) is already fitted with the test case.

    The test case: https://www.icloud.com/iclouddrive/0RmbWZrmOikBLoB9osy1odzUw#ReportToNghia_-_RigidTransform

    Reply

    1. Just did a quick test with your dataset with my code. It seems to work. This is the Python results

      >>> A
      array([[0, 0, 1],
      [0, 1, 0],
      [0, 0, 0]])
      >>> B
      array([[0, 0, 0],
      [0, 1, 0],
      [0, 0, 1]])
      >>> R, t = rigid_transform_3D(A, B)
      det(R) < R, reflection detected!, correcting for it ... >>> R@A -B
      array([[ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
      [ 0.00000000e+00, 0.00000000e+00, -1.21168839e-16],
      [ 0.00000000e+00, -1.21168839e-16, 2.22044605e-16]])

      Reply

  191. I’ve got the python program running. Thankyou! But I need some help in changing it to read the xyz points from a file.

    This works but I’d rather read from a file:
    A = np.array([[0,16,0],
    [0,0,12],
    [0,0,0]])
    B = np.array([[0.23818535,16.2065245,-0.15620586 ],
    [-0.28949261,0.26813408,11.69519908],
    [0.18953994,-0.64783536,0.64956234 ]])

    Fileinputxyz.csv
    P1, x, y, z
    P2, x, y, z
    P3, x, y, z

    The trouble is the array requires the points to be transposed into a different shape.

    P1, P2, P3
    x1, x2,x3
    y1,y2,y3
    z1,z2,z3

    note: apologies for previous post CR/LF was removed not sure if this post fixes it hope it does.
    Any ideas on how to get this to work? Any help would be appreciated. Thanks

    Reply

  192. Hello Nghia Ho, congrats, your article made it into the top of search engines like google and bing. Thanks for the simple explanation of the normal case. However your fix for the mirror case got me wondering and googling more, finding Kabsch Algorithm on Wikipedia https://en.wikipedia.org/wiki/Kabsch_algorithm which has a simpler – and maybe even better? – solution for the mirror case. My intuition is that in case of mirroring we want to mirror the smallest axis of the correlation matrix. When doing another SVD on R the order of axes is likely random and depending on the implementation of SVD?

    Reply

    1. The mirror case is something I have not spent too much time on despite seeing it quite often. If you come across a robust solution please let me know!

      Reply

      1. In my opinion I did just that. Any specific reason why you assume Kabsch algorithm as described by Wikipedia is not a robust solution?

        Reply

  193. Thank you for the explanation and code! It works very well.

    I have an additional question:
    How to calculate the deviation in X-direction e.g. from green point B to green point A (after optimal rotation and translation)?

    The deviation in X-direction should be very small and is formed from the difference of green point B and point A (after rotation and translation)?

    Many thanks in advance.

    Reply

  194. Hi Nghia Ho, thank you for this amazing tutorial. I am trying to implement the algorithm to align 3D points detected from depth sensors. I am getting a large rmse error on the first go. I then apply the calculated rigid transform to data set A and re-calculate the rigid transform using the new data set A and the original data set B. Can you tell me if this procedure should result in the data sets converging? When I attempt to implement this procedure, the rotation matrix and translation vector become negligible after the first iteration even though the point sets are not close to matching. This results in the point sets never converging. Have you encountered a situation like this? Thanks again.

    Reply

  195. You must be Jay’s buddy. Hello There!
    I am debugging the 2D to 2D transformation between two camera views which I’ve received. The transformation parameters are off. Going to fix the transformation with your code.
    Thanks!

    Reply

  196. Hi,

    The algorithm doesn’t seem to perform well on clockwise rotations. For example, given those 2 data points.

    B_points{{-0.5,0,0}, {0.5,0,0}};
    A_points{{-0.5,-0.5,0}, {0.5,0.5,0}};

    It finds the following rotation matrix before correction for reflection.

    0.707107 0.707107 0
    0.707107 -0.707107 0
    0 0 1

    and then the correction leads to this matrix

    0.707107 0.707107 0
    0.707107 -0.707107 0
    0 0 – 1

    whose determinant is not 0 anymore, but the rotation is wrong and it added another flip over the x,y plane.

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *