Last Updated on February 16, 2012 by nghiaho12
I’ve been mucking around with a multivariate decision tree for the past few days in Octave. Mostly out of curiosity. It’s basically a decision tree that uses a hyper plane to split the data at each node, instead of splitting at a single attribute. For example, say we have 2D data (x,y), a node in a standard decision tree might look like
if
where as a multivariate might be
if
The idea seems to have been around since the early 90s but for some reason you don’t hear about them nowadays. Maybe for good reason? Either way still an interesting idea. My implementation uses RANSAC to find a good hyper plane to split the data and uses the ‘Information Gain’/Entropy formula to measure the “goodness” of the hyper plane.
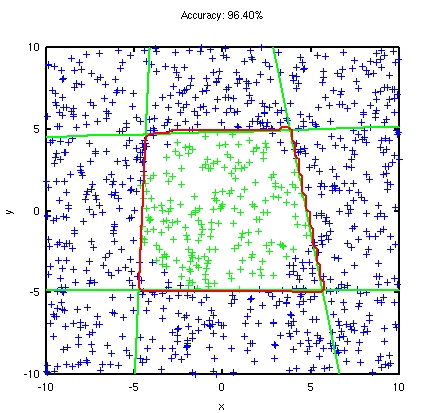
Below are two simple synthetic test data that a decision tree and linear classifier might have trouble with, but when combined together they perform quite well. The green lines are the individual linear decision boundaries at each node and the red is the final boundary. The green samples are labelled “positive” and blue is “negative”. The accuracy of the classification is shown in the title of the graph.
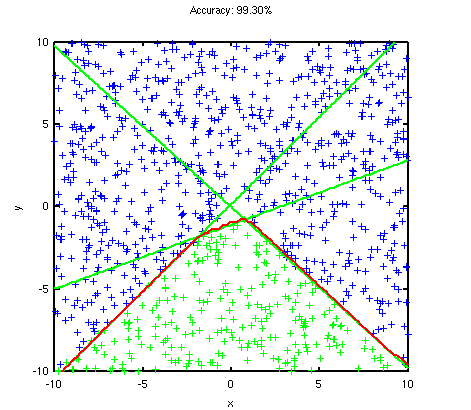
The first dataset above cannot be separated using a single linear decision boundary, where as a decision tree on the other hand will probably zig-zag along the diagonal boundary producing a bigger tree than necessary. The multivariate decision tree on the other hand separates the data in 3 cuts. It is close to what I would consider the best, which would be 2 cuts along the diagonal boundaries. This is interesting, because it seems to suggest that to get the best decision boundary a sub-optimal cut might be required at some stage! I wonder if there’s a way to re-visit the boundary lines and simplify them …
The second dataset consists of positive samples shaped in a circle enclosed by negative samples. Pretty typical synthetic dataset. Again, no single linear decision boundary will separate this. But a decision tree will probably produce similar result to what I got given only 4 cuts as well.
Download
Download the Octave script. Might need to do right click save as.
Extract and call Run.m, that’s capital R and not ‘run’ !
Very cool! I think this is a big idea that the ML community should pay attention to. It’s sost of a decision tree with a perceptron classifier.
How do you determine which splitting planes to use? Obviously the one with the highest information gain, but which algorithm to use to find that? Gradient descent? Simulated annealing?
I actually just do a RANSAC, pick random points and find the plane with the highest information gain.