Last Updated on September 23, 2011 by nghiaho12
This is an update on my camera lens fail post, where my Tamron rear lens cap got permanently stuck on a Samyang lens. Here is the picture story of how it went down.
Last Updated on September 21, 2011 by nghiaho12
Over the weekend I was shooting with my new Samyang 85mm F1.4 and decided to swap it over with a Sigma 30mm F1.4 to do wider shooting. I had a Tamrom rear lens cap in the bag so I used that. I’m lazy when it comes to camera, I just re-use the same rear lens cap for every lens, one size fit all. Never had an issue until recently. The picture below summarises what happened:
So what now? My initial plan is to use the CNC as shown below.
What could go wrong? Well, we’ll find out soon enough!
Last Updated on September 21, 2011 by nghiaho12
I’ve recently discovered this cool piece of open source software called Maxima. For those unfamiliar, it is a Computer Algebra System (CAS). You can express maths problem using symbols (as oppose to numerical values only) and apply common maths operations like integration, differentiation, matrix manipulation, finding roots, solving for x, simplification etc. etc. to name a few. In fact, it could probably do most of your calculus homework for you, provided the teacher overlooks the fact that you didn’t show any working step.
Maxima operates on the command line but I tend to use the GUI frontend wxMaxima.
Here’s a programming scenario, you need to do a simple matrix operation, like an inversion of a 3×3 matrix to solve a linear problem. You want it fast but don’t want the hassle of linking to an external library, for whatever reason. Sure, you could do a quick Google and probably find an answer or use it as an excuse to play with Maxima. Here is how to do this in wxMaxima.
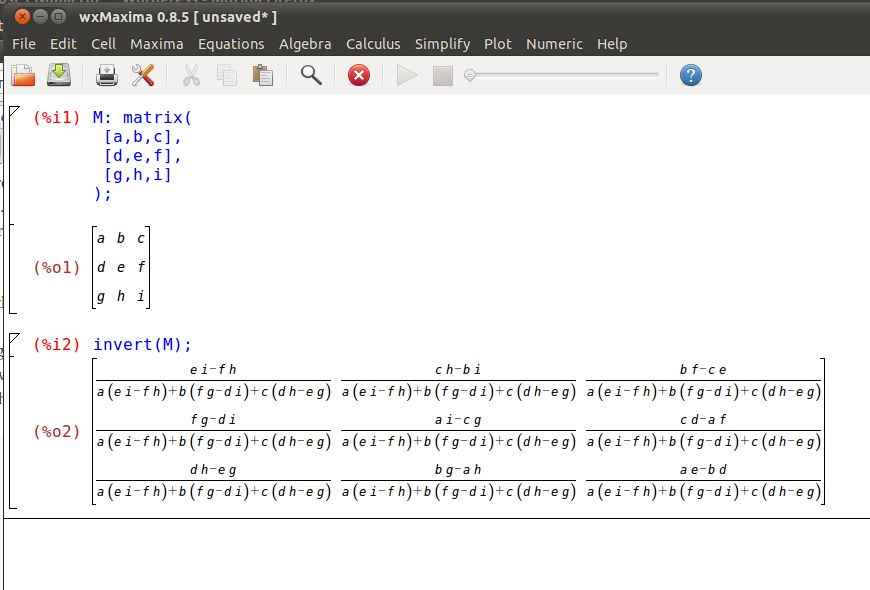
M is the 3×3 matrix with each element index by some letter. The output can now be translated directly into C, C++ code or whatever your favourite language is. Notice how the denominator is all the same, so you can improve efficiency by storing it into a variable. You can also check if the denominator is near zero, which would indicate a singular matrix that can’t be inverted.
Eigenvalues of a 3×3 matrix? Sure !
Err okay, maybe not such a great idea.
Need to solve Ax = b? Just re-arrange to x = invert(A)b and you got your answers. You probably only need one IF statement and the rest are maths operation. Not a single FOR loop. How’s that for lean and mean code.